Vorlesung 6 ComputationalEngineering
(:requiretuid:)
Einführung in Computational Engineering – Vorlesung 6
Autoren: Andrej Felde und Thomas Hesse
Folien zur Vorlesung 6: Link
Folien zur Vorlesung 6 mit Annotationen: Link
Aufzeichnung der Vorlesung 6 mit Dozent: Link
Aufzeichnung der Vorlesung 6 ohne Dozent: Link
Übung 5: Link
Zahlendarstellung
Reelle Zahlen werden auf Computern als normalisierte Gleitpunktzahlen dargestellt. Eine normalisierte Gleitpunktzahl wird allgemein definiert durch:
Dabei sind die Zahlen wie folgt definiert:
- Basis
(Dezimalsystem 
und im Binärsystem 
)
- Exponent
ist eine ganze Zahl und ist durch 
beschränkt. (Bei 
wäre 
)
- Ziffern
stellen die Zahlen der Zahl dar. (Bei 
wäre 
und 
- Die Länge der Mantisse wird durch
beschrieben. (Bei 
wäre 
)
- Die Mantisse selbst besteht aus den Ziffern
Man kann sich die Darstellung anhand einer normalisierten Dezimalzahl verdeutlichen. Nur die erste Stelle vor dem Dezimalpunkt ist ungleich Null, wenn die Zahl selbst nicht die Null ist. Alle anderen Stellen vor dem Dezimalpunkt (Dezimalkomma) sind gleich Null.
Auf heutigen Computern werden reelle Zahlen allerdings als Binärzahlen dargestellt. Zudem besteht die gängige Speicherwortlänge aus 32 Bit. Damit ergibt sich eine Aufteilung von einem Bit für das Vorzeichen, 8 Bit für den Exponenten und 23 Bit für die Mantisse selbst. Der Wert der Zahl kann dann mit 
Stellt man mehr Bits für den Exponenten 
bereit ergibt sich ein größerer Bereich der dargestellt werden kann. Stellt man hingegen mehr Bits für die Mantisse 
bereit, so können die Zahlen genauer dargestellt werden. Zur Standardisierung wird der IEEE 754 Gleitpunktstandard verwendet.
IEEE 754 Gleitpunktstandard
Beim Gleitpunktstandard wird festgelegt wie viele Bit für den Exponenten bzw. für die Mantisse bereitgestellt werden. Bei einfacher Genauigkeit (single precision) hat der Exponent 8 Bit und die Mantisse 23 Bit. Bei doppelter Genauigkeit (double precision) hat der Exponent 11 Bit und die Mantisse 52 Bit. Außerdem wird das oberste Bit der Mantisse also 
weggelassen, da dieses implizit immer da ist, wenn die Zahl selbst ungleich Null ist. Zudem wird der Bias eingeführt. Der Bias dient zur Verhinderung von negativen Exponenten sowie zur Verhinderung von zusätzlichen Aufwand bei der Darstellung. Dazu wird zu einem Exponenten 
der Bias 
addiert. Dieser Wert 
wird dann gespeichert. Bei einfacher Genauigkeit ist der Bias 
und bei doppelter Genauigkeit ist der Bias 
.
Sonderfälle
Ist die Zahl selbst die Null wird diese als reservierter Sonderfall behandelt. Dabei sind dann alle 32-Bit (bei single precision) gleich 0. Ein Überblick über die Werte kann man auch folgender Tabelle entnehmen.
Eigenschaften
Zusammenfassend kann man folgende Eigenschaften aufzählen
- Es gibt nur endlich viele Gleitpunktzahlen
- Es gibt keine beliebig großen und keine beliebig kleinen (positiven) Gleitpunktzahlen
- Es gibt keine beliebig nahe benachbarte Zahlen
- Die Gleitpunktzahlen sind ungleichmäßig verteilt
- Summe/Differenz, Produkt/Quotient von Gleitpunktzahlen müssen i.Allg. gerundet werden
Rundungsfehler
Wie im vorherigen Kapitel bereits gezeigt wurde gibt es nur endlich viele Gleitpunktzahlen und nach Summe / Differenz, Produkt / Quotient muss im Allgemeinen gerundet werden. Rundungsfehler sind jedem ein Begriff, allerdings ist die Frage wie sich Rundungsfehler auswirken. Allgemein lässt sich Runden wie folgt definieren:
.
Dabei steht 
für eine Gleitpunktzahl. Da das Ergebnis einer arithmetischen Operation im Allgemeinen keine Maschinenzahl ist, muss das Ergebnis gerundet werden. Beim Runden kann man den relativen Rundungsfehler bestimmen. Die relative Maschinengenauigkeit 
ist zum Beispiel auch nichts anderes als der maximale relative Rundungsfehler. Zudem kann man auch den absoluten Rundungsfehler bestimmen. Dieser gibt einfach nur die Abweichung der gerundeten Gleitkommazahl zur reellen Zahl an. Den relativen Rundungsfehler bestimmt man durch:
Es kann festgehalten werden, dass für Gleitpunktarithmetik weder das Assoziativ- noch das Distributivgesetz gelten. Dies kann man sich durch die Addition von zwei sehr kleinen und ähnlichen Zahlen x,y mit einer sehr großen Zahl z verdeutlichen. Addiert man nun zuerst x und y kommt eine potenziell größere Zahl raus. Diese hat dann, da sie näher an y liegt, auch einen größeren Einfluss auf das Ergebnis. Addiert man nun x oder y zuerst mit z hat die sehr kleine Zahl kaum Einfluss auf das Ergebnis. Dabei wird durch Runden und durch die beschränkte Größe der Mantisse das Zwischenergebnis kaum geändert. Das Gleiche passiert dann bei der Addition der zweiten kleinen Zahl.
Ein kleines Beispiel wie sich Rundungsfehler auswirken können sieht man auch noch in folgendem Beispiel, welches bereits aus der Vorlesung bekannt sein sollte. Weitere Bespiele kann man auch noch hier [1] finden.
Auslöschung
Die Auslöschung beschreibt den Verlust von Bits, die beim Speichern einer sehr großen oder sehr kleinen Zahl auftreten. Auslöschung kann durchaus auch bei Gleitpunktarithmetischen Operationen auftreten. Als Beispiel nehme man Zahlen an, die durch eine Reihe approximativ dargestellt werden, so in etwa 
.
Kondition
Die Kondition beschreibt wie sich Rundungsfehler auf eine Funktion 
auswirken. Dabei versteht man unter "schlecht konditioniert", dass kleine Änderungen in x große Änderungen in bewirken. Die Konditionszahlen sind die Beträge der Verstärkungsfaktoren zum relativen Fehler von y. Der relative Fehler ist mit Taylorentwicklung gegeben durch:
Damit sind die Konditionszahlen gegeben durch:
Sind die Konditionszahlen "groß", ist das Problem "schlecht konditioniert". Sind die Konditionszahlen 
hingegen "klein", ist das Problem "gut konditioniert". Das Besondere an den Konditionszahlen ist, dass diese nur von den Eigenschaften der Funktion 
abhängen. Es besteht keine Abhängigkeit zur Auswertungsart oder wie die Rechnerarithmetik aussieht!
Entsprechend kann man sich vorstellen , dass wenn 
Eingabefehler nicht verstärkt werden und wenn 
Eingabefehler verstärkt werden.
Numerische Stabilität
Die numerische Stabilität ist nochmal eine Verschärfung zur Kondition. Unter der numerischen Stabilität versteht man wie Eingabefehler das Ergebnis in Hinblick auf die Auswertung beeinflussen, selbst wenn das Problem gut konditioniert ist.
- Ein Berechnungsverfahren für nennt man numerisch stabil, falls die relevanten Eingabefehler nicht verstärkt werden
- Ein Berechnungsverfahren, nennt man numerisch instabil, falls große relative Fehler im Ergebnis erzeugt werden
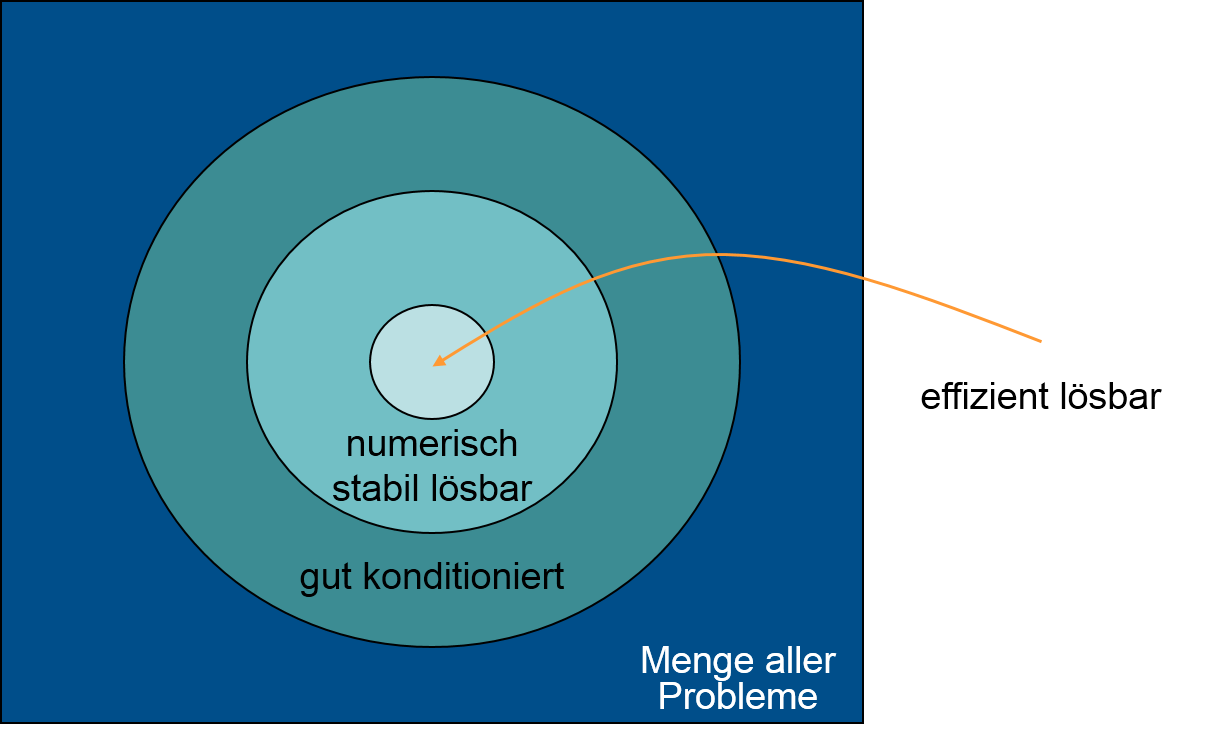
Man sieht, dass gut konditionierte Probleme starke Rundungsfehler aufweisen können, wenn sie numerisch instabil sind. Bei der numerischen Stabilität gibt man also eine Aussage über die Ergebnisqualität nach der Auswertung durch einen Rechner!
Selbstest
Links auf dieser Seite
Feedback
Bei Fehlern oder Anregungen zu dieser Seite schicken Sie bitte eine Email an andrej.felde@stud.tu-darmstadt.de oder thomas.hesse@stud.tu-darmstadt.de.
