(:requiretuid:)

Einführung in Computational Engineering – Vorlesung 2

Autoren: Andrej Felde und Thomas Hesse

Folien zur Vorlesung 2: Link
Folien zur Vorlesung 2 mit Annotationen: Link
Aufzeichnung der Vorlesung 2 mit Download Button: Link
Übung 1: Link

In dieser Vorlesung wiederholen wir die Begrifflichkeit diskreter Modelle und beschäftigen uns anschließend hauptsächlich mit der ereignisdiskreten Simulation eines Warteschlangenmodells. Einen Überblick über alle relevanten Begriffe zur ereignisdiskreten Simulation findet man hier [1]. Hier wird zudem ein Algorithmus zur ereignisdiskreten Simulation eines Warteschlangenmodells vorgestellt. In Vorlesung 3 [2] wollen wir dann das Warteschlangenmodell verallgemeinern. Danach schauen wir uns ein weiteres Modell, das sogenannte Petrinetz, zur (ereignis)diskreten Modellierung an. Anschließend definieren wir relevante Eigenschaften für Petrinetze.

Ereignisdiskrete Simulation eines Warteschlangenmodells

Nachdem in der Vorlesung diskrete Modelle wiederholt wurden, wird hier die Kenntnis darüber vorausgesetzt. (Bei Problemen bitte erneut mit Vorlesung 1 [3] auseinandersetzen.) Wir nehmen Bezug auf die vorherige Vorlesung 1 [3] in der wir darüber gesprochen haben, wie wir ein Modell für eine konkrete Problemstellung herleiten. Im folgendem betrachten wir das konkrete Beispiel eines Supermarktes.

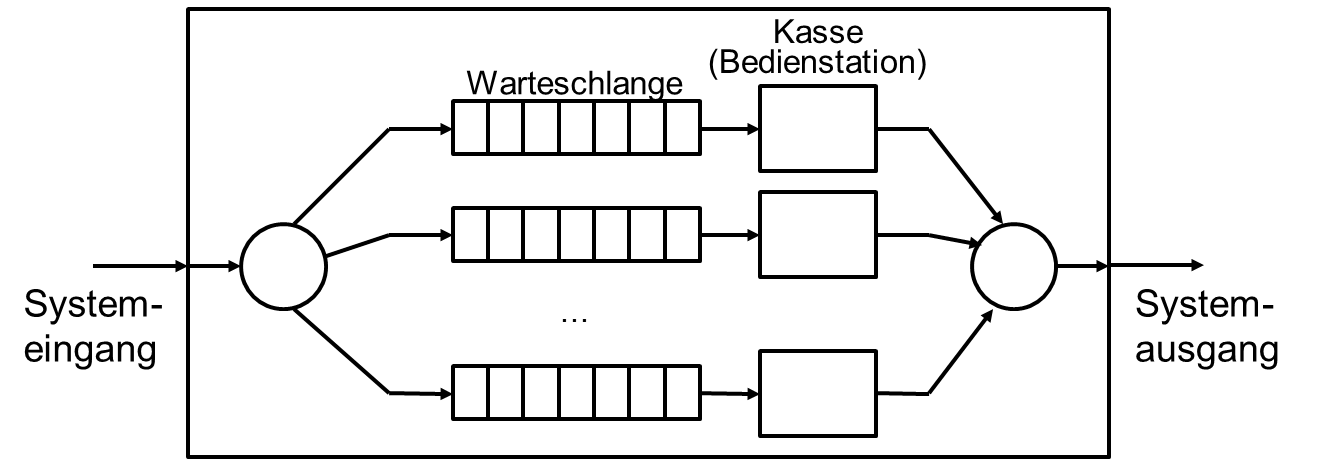
Abbildung 1. Abstrahierte Darstellung von Warteschlangen mit Kassen. Der Sachverhalt
in diesem Bild modelliert das System an sich.

Zuerst abstrahieren wir den Sachverhalt und blenden damit unnötige Details aus. Weiter versuchen wir für die Simulation wichtige Objektklassen und Attribute zu identifizieren und zu benennen (mathematische Modellbildung). Wichtige Objektklassen wären für unser Modell Kunde/in, Kasse und Kassierer/in. Möglicherweise relevante Attribute für Kunden wären dann z.B. Anzahl der Artikel, jeweils Eintrittszeitpunkt und Austrittszeitpunkt in und aus dem System. Etwas einfacher wären die Attribute für die Kasse (offen oder geschlossen) und für die Kassierer/innen (routiniert oder langsam). In Abbildung 1. erkennen wir, dass die jeweilige Kasse ihre Warteschlange sequentiell abarbeitet. Somit könnten wir für jede einzelne Kasse z.B. den Durchsatz erhöhen und somit das System optimieren, indem man mittels Simulation herausfindet wie viele Kassen bei wie vielen Kunden gleichzeitig geöffnet sein müssten.

Discrete-event simulation (DES Algorithmus)

Der Algorithmus zur ereignisdiskreten Simulation bietet sich sehr gut für die Simulation von Warteschlangenmodellen an. In der Simulation selbst geht man davon aus, dass zwischen den Ereignissen keine Änderungen geschehen. Daher kann man von einem ereignisdiskreten Zeitpunkt zum nächsten springen. Dies wird in der folgenden Abbildung 2. dargestellt. Den Algorithmus selbst, finden Sie hier [4].

Abbildung 2. Ereignisdiskrete "'Zustandssprünge'" auf der Zeitachse. Die "'Zustandssprünge'" sind
hier als Zustandsübergänge zu verstehen.

Petrinetze

Petrinetze können diskreter oder kontinuierlicher Natur sein. In dieser Vorlesung betrachten wir jedoch nur den diskreten Fall (insbesondere den ereignisdiskreten Fall) von Petrinetzen um einen guten Einsteig in das Thema zu gewährleisten.
Ein Petrinetz ist ein System bestehend aus dem folgendem Tupel . Die Bedeutung der einzelnen Parameter wird in folgender

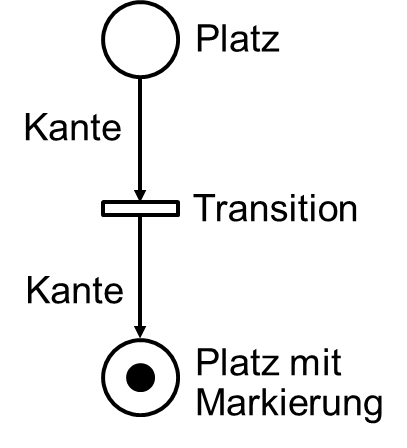
Auflistung erklärt. Dafür sei .

– endliche Menge aller Plätze
– endliche Menge aller Transitionen
– endliche Menge gerichteter Kanten
– Menge der Platzkapazitäten
– Anfangsmarkierungen der Plätze

Der Zustand eines Petrinetzes wird durch die Menge der Markierungen ausgedrückt. Zudem hat ein Petrinetz verschiedene Eigenschaften, welche hier [5] genauer erklärt werden. Nun wollen wir uns Petrinetze etwas praktischer anschauen, um zu verstehen wie diese funktionieren. Es ist wichtig zu wissen, dass bei einem Petrinetz eine Transition nur dann schalten kann (auch "feuern" genannt), wenn alle Eingangsplätze (damit sind Plätze gemeint, die eine Kante zur Transition besitzen) mit mindestens einer Markierung belegt sind. Anschließend wird aus jedem Eingangsplatz eine Markierung entnommen und in jedem Ausgangsplatz eine Markierung hinzugefügt.

Eingangsplätze („fan-in") – Plätze, die eine Kante zu der Transition besitzen
Ausgangsplätze („fan-out") – Plätze, mit einer Kante von der Transition zum Platz

Hinweis: Eingangs- bzw. Ausgangsplätze beziehen sich stets auf eine bestimmte Transition. Jede Transition kann verschiedene Eingangs- und Ausgangsplätze haben.

Petrinetz Beispiel

Als Beispiel betrachte man folgendes Petrinetz:

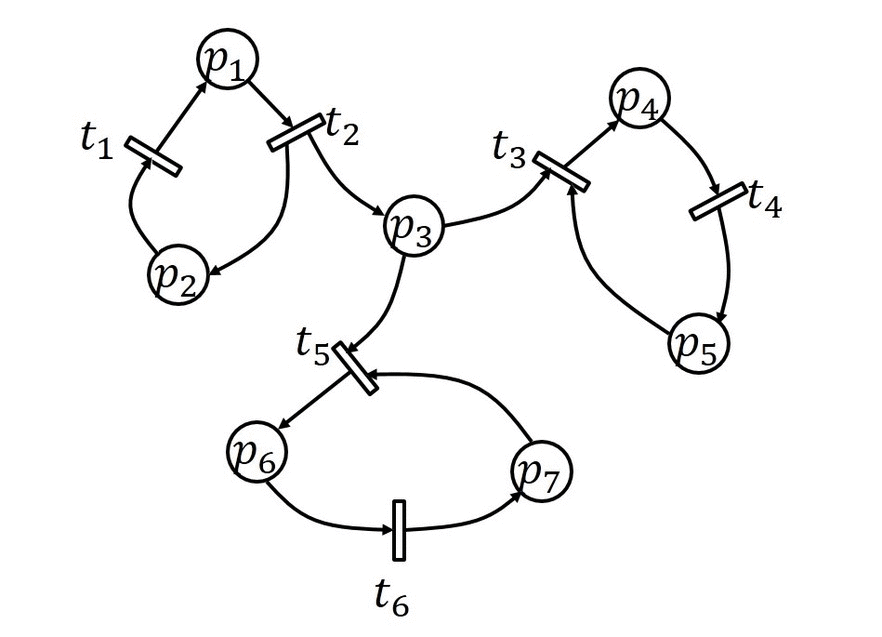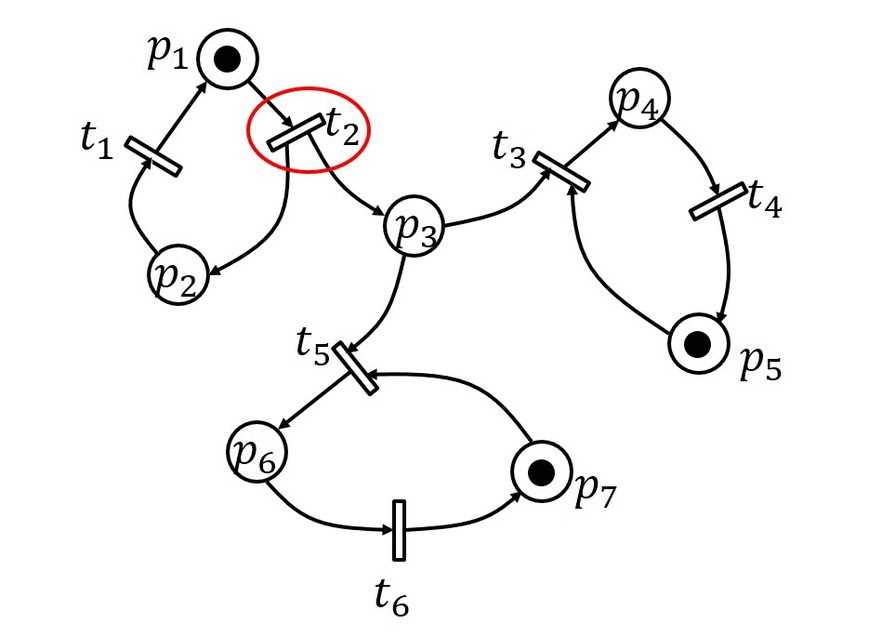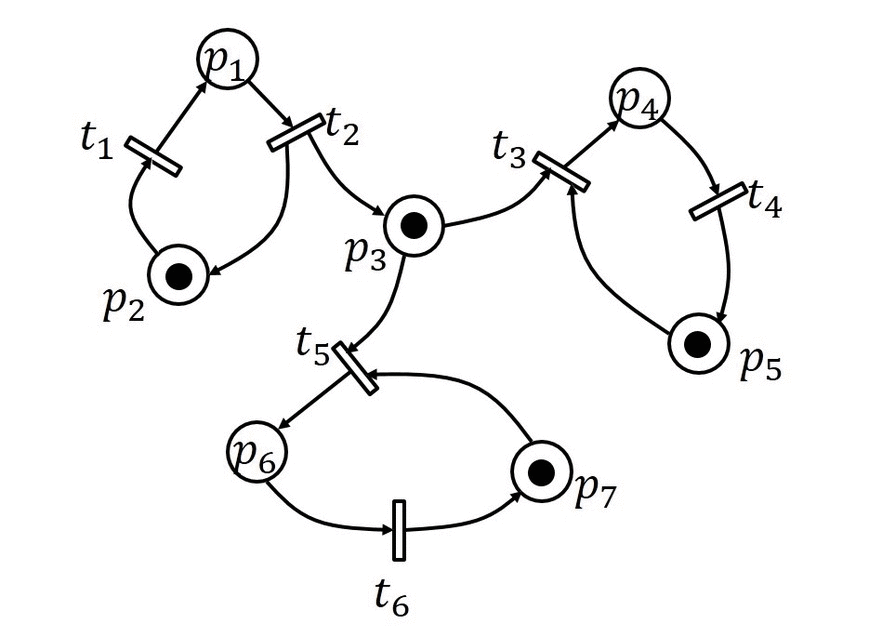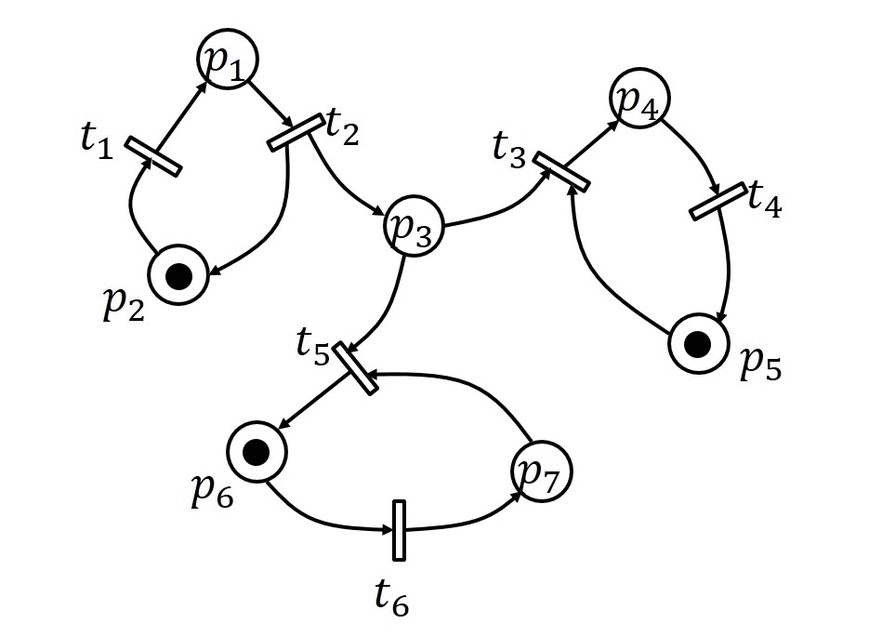
Man sieht ein Petrinetz mit sieben Plätzen und sechs Transitionen. Zur Initialisierung sind die Plätze und markiert. Bei Initialisierung gilt also . Feuert nun muss eine Markierung von entfernt und jeweils eine Markierung bei und hinzugefügt werden. Nun können als auch feuern. Im Beispiel feuert . Dies führt dazu, dass eine Markierung bei den Plätzen und entfernt und bei hinzugefügt wird. Für sind und Eingangsplätze und ein Ausgangsplatz.

Inzidenzenmatrix

Eine Inzidentenmatrix beschreibt die Beziehung der Knoten und Kanten in einem Petrinetz. Genauer gesagt beschreibt dieses welche Plätze nach dem Schalten einer Transition eine weitere Markierung erhalten und von welchen Plätzen eine Markierung entnommen wird. Die Spalten einer Inzidenzenmatrix stehen für die jeweiligen Transitionen und die Zeilen für die jeweiligen Plätze eines Petrinetzes. Grundsätzlich kann man eine Inzidenzenmatrix in folgende Matrizen aufteilen:

Matrix („post-weights“) besteht aus Verbindungen
Matrix („pre-weights“) besteht aus Verbindungen

Intuitiv beschreibt die Matrix welche Plätze nach dem Schalten einer Transition eine weitere Markierung erhalten und Matrix welche Plätze vor dem Schalten einer Matrix mindestens eine Markierung enthalten haben. Aus der Differenz der „post-weights“ und der „pre-weights“ ergibt sich die Inzidenzenmatrix .

Beispiel

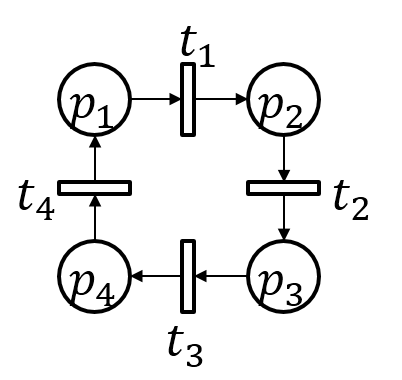
Allgemein lässt sich die Größe der Inzidenzenmatrix über die Anzahl der Transitionen und Plätze ermitteln. Die Einträge ergeben sich über den sogenannten „fan-in" und „fan-out". Das Petrinetz besitzt jeweils vier Plätze und vier Transitionen. Damit ergibt sich eine 4x4-Matrix mit folgenden Werten:

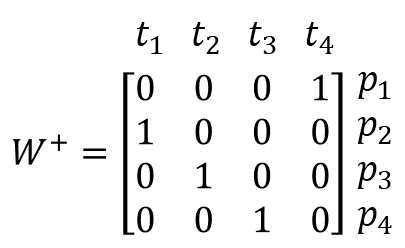
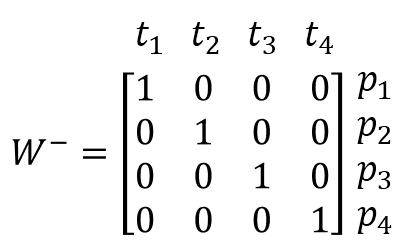
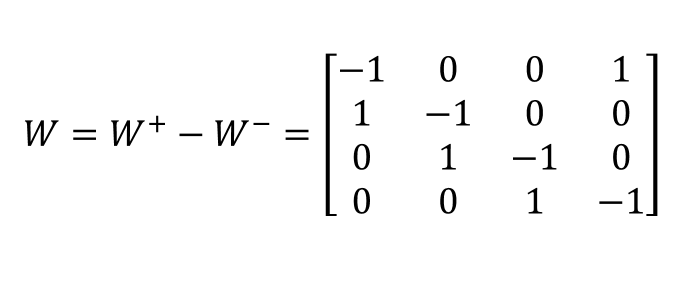
Und wie wir gesehen haben, ergibt sich dann aus der Differenz der „post-weights" und der „pre-weights" dann die resultierende Inzidenzenmatrix:

Selbstest

Als Simulation wird ein virtuelles (im Allgemeinen rechnergestütztes) Experiment am Modell bezeichnet.
Mit einer ereignisdiskreten Simulation (DEVS) kann ein zeitlicher Verlauf von Zustandsgrößen errechnet werden.
Bei ereignisdiskreten Modellen können sich Zustandsgrößen stetig ändern.
Bei einem ereignisdiskreten Modell kann in endlicher Zeit nur eine endliche Anzahl von Zustandsänderungen auftreten.
Jedes Petrinetz ist ein bipartiter Graph.
In eine Transition eines Petrinetzes können mehrere Kanten hineinführen, aber immer nur eine heraus.
Die Inzidenzmatrix eines Petrinetzes gibt auch Auskunft über dessen aktuelle Markierungen
Verschiedene Petrinetze können die gleiche Inzidenzmatrix haben

(:antwortchecker:)

Links auf dieser Seite

[1] Terminologie
[2] Vorlesung 3
[3] Vorlesung 1
[4] Discrete-event simulation Algorithmus (Ereignisdiskreter Simulationsalgorithmus)
[5] Eigenschaften von Petrinetzen

Feedback

Bei Fehlern oder Anregungen zu dieser Seite schicken Sie bitte eine Email an andrej.felde@stud.tu-darmstadt.de oder thomas.hesse@stud.tu-darmstadt.de.