(:requiretuid:)

Einführung in Computational Engineering – Vorlesung 3

Autoren: Andrej Felde und Thomas Hesse

Folien zur Vorlesung 3: Link
Aufzeichnung der Vorlesung 3: Link
Aufzeichnung der Vorlesung 3 mit Download Button aber ohne Dozent: Link
Übung 2: Link

Zufallszahlen und lineare Kongruenz

Bei dem linearen Kongruenzgenerator handelt es sich um eine Methode um Zufallszahlen im Rechner zu erzeugen. Zufallszahlen sind für Simulationen insofern relevant, da man meist viele Eingaben braucht und diese aufgrund von Empirie durchzuführen ist oft zu zeit-intensiv oder zu kosten-intensiv. Daher betrachten wir zufällig generierte Werte, welche dann anschließend (und auf der Problemstellung basierend) durch eine spezifische Wahrscheinlichkeitsverteilung angepasst werden kann. Daher zeigen wir jetzt erst einmal wie man über den linearen Kongruenzgenerator Zufallszahlen erzeugt:

Wahl eines Startwertes, dem sogenannten seed. Mathematisch notieren wir dies als .
Erzeugen von mehreren Zufallswerten basierend auf dem vorherigem Zufallswert mit .

Dabei ist und einmal fest gewählt und jeweilig ein Multiplikator und ein Inkrement, welche zusätzlich noch mehr Zufall erzeugen sollen. beschreibt hier den Modulus. Der interessierte Leser entdeckt dabei auch natürlich, dass es sich hierbei um viele Äquivalenzklassen handelt und somit nicht mehr Zufallszahlen als Äquivalenzklassen generiert werden können. Anschließend können diese Werte nun einer Verteilung zugeordnet werden. Außerdem lässt sich mithilfe des linearen Kongruenzgenerator eine Zufallsvariable definieren.

Wahrscheinlichkeit

Die Wahrscheinlichkeit für das Eintreten eines Ereignisses lässt sich durch die Wahrscheinlichkeitsfunktion mit Zufallsvariable bzw. beschreiben. Für die Wahrscheinlichkeitsfunktion gilt und die Summe aller Wahrscheinlichkeiten ergibt immer 1.

– Wahrscheinlichkeit des Ereignisses .
– Wahrscheinlichkeit, dass beide Ereignisse und eintreten.
– Wahrscheinlichkeit, dass eintritt, unter der Bedingung, dass bereits eingetreten ist. (bedingte Wahrscheinlichkeit)
– Multiplikationssatz für bedingte Wahrscheinlichkeiten.

Sind zwei Ereignisse und voneinander unabhängig und gilt für die einzelnen Wahrscheinlichkeiten dann gilt:

Verteilungen

Die Verteilung einer Zufallsvariable kann mit einer Verteilungsfunktion beschrieben werden. Alle möglichen Wahrscheinlichkeiten einer Zufallsvariable können dann mithilfe der Verteilungsfunktion berechnet werden. Verteilungsfunktionen können sowohl diskret als auch kontinuierlich verteilte Zufallsvariablen beschreiben und es gilt allgemein:

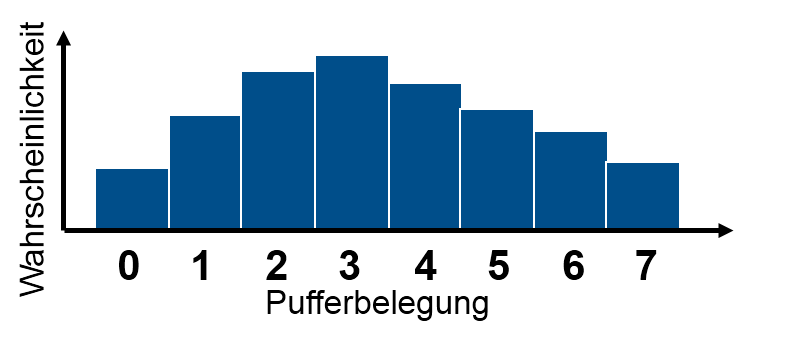
Für diskret verteilte Zufallsvariablen kann man die einzelnen Wahrscheinlichkeiten angeben. Für die Verteilungsfunktion folgt:

Ein Beispiel für eine diskret verteilte Zufallsvariable wäre die Pufferbelegung.

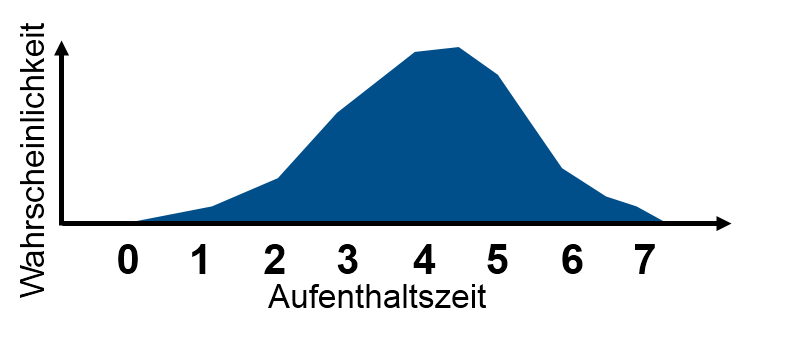
Für kontinuierlich verteilte Zufallsvariablen kann man die Verteilungsfunktion über die Wahrscheinlichkeitsdichte angeben. Für die Verteilungsfunktion folgt dann:

Ein Beispiel für eine kontinuierlich verteilte Zufallsvariable wäre die Aufenthaltszeit einer Entität im Puffer.

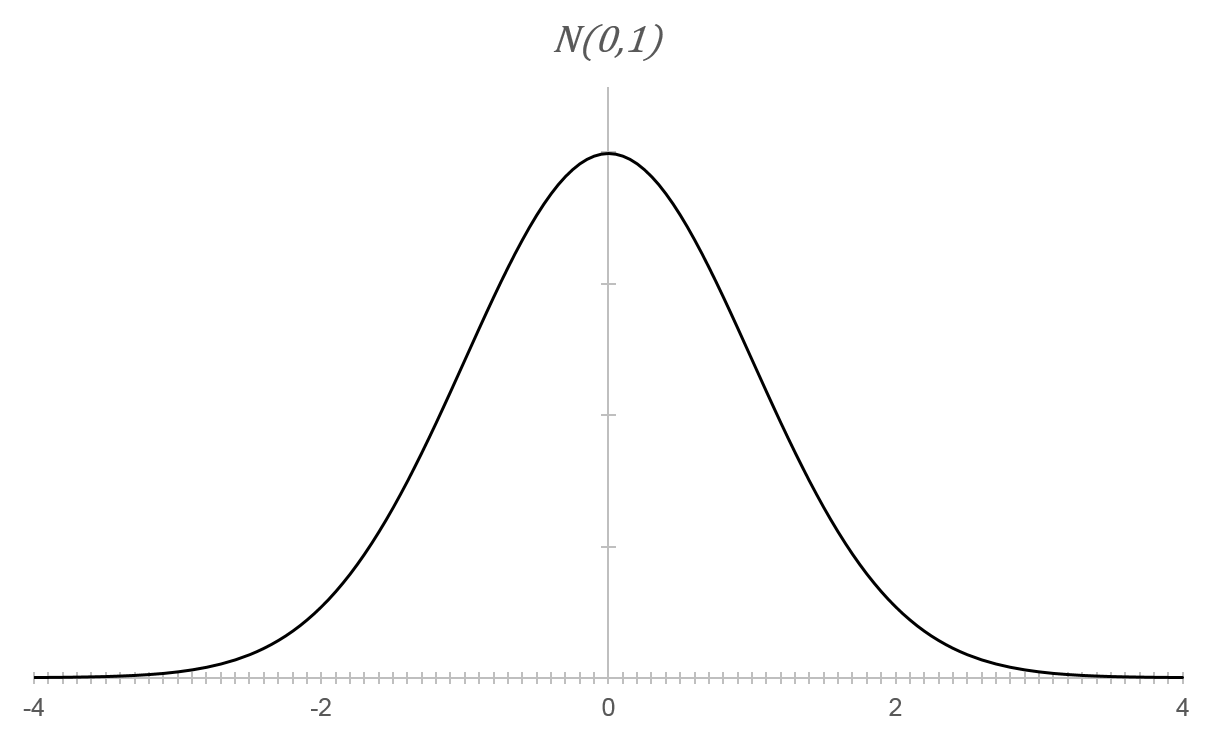
Normalverteilung

Abweichungen vom Mittelwert lassen sich besonders gut durch die Normalverteilung beschreiben. Eine Zufallsvariable ist normalverteilt mit Parametern und , kurz . Ist eine Zufallsvariable normalverteilt, so schreibt man auch . Die Dichtefunktion der Normalverteilung lautet:

Dabei steht für den Erwartungswert und für die Varianz. Sind der Erwartungswert und die Varianz spricht man von einer Standard-Normalverteilung.

Exponentialverteilung

Nur die exponentielle Verteilungsfunktion ist ohne Gedächtnis mit Markov Eigenschaft. Daher eignet sie sich besonders zufällige Zeitintervalle zu beschreiben. Eine Zufallsvariable mit Parameter , kurz heißt exponentialverteilt. Ist eine Zufallsvariable exponentialverteilt, so schreibt man auch . Die Dichtefunktion der Exponentialverteilung lautet:

Allgemeines Warteschlangenmodell

Das Warteschlangenmodell (Warteschlangentheorie) kann in verschiedensten Gebieten genutzt werden. Warteschlangen treten überall im Alltag auf. Beispiele dafür wären:

Studenten in der Mensa
Autos im Stau oder vor der Ampel
Kunden vor der Supermarktkasse
...

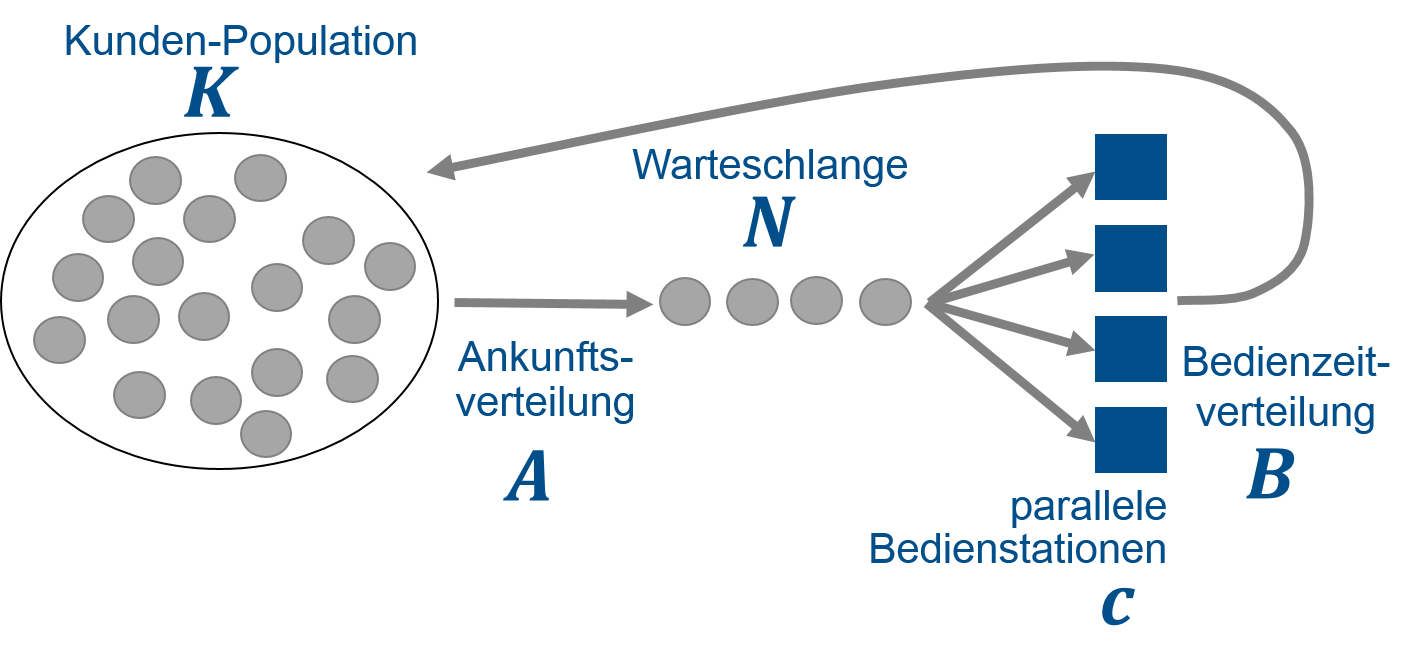
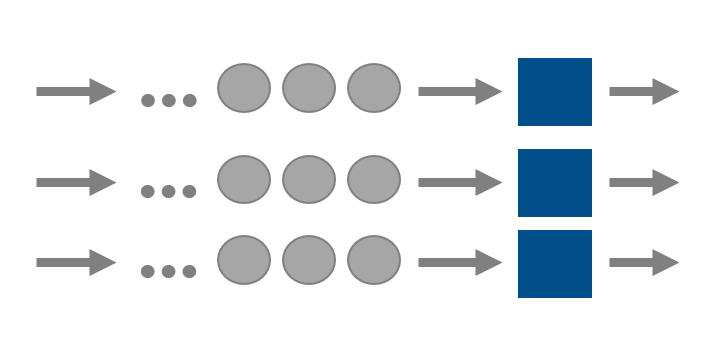
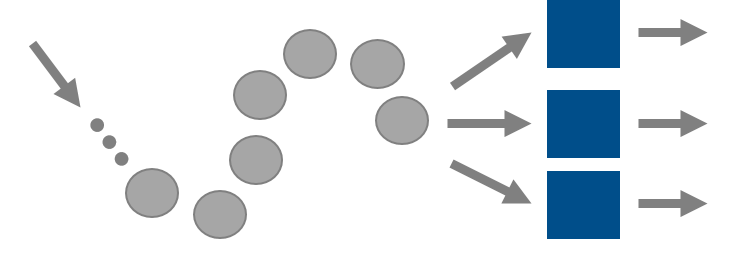
Die genannten Beispiele haben alle bestimmte Gemeinsamkeiten. Ein Student, Auto, Kunde oder allgemein eine Entität möchte von einer Bedienstation bearbeitet werden. In unseren Beispielen wären das die Essensausgabe in der Mensa, eine Ampel oder die Kasse im Supermarkt. Ist die Bedienstation belegt muss die Entität in einer Warteschlange oder im Stau auf die Bearbeitung warten. Ziel des Warteschlangenmodells ist es den Ablauf zu optimieren oder nachzuvollziehen, bei bekanntem Szenario oder bei unbekanntem Szenario eben solch einen Sachverhalt vorherzusagen. Bei einem Supermarkt könnte man so feststellen was die optimale Anzahl an Kassen wäre, ohne zu viel für Kassierer/innen zu bezahlen bzw. ohne die Kunden zu lange warten zu lassen. Oder man kann vorerst feststellen, wie dieses Szenario im Allgemeinem abläuft. Interessant ist auch solch ein Szenario vorherzusagen, da man im richtigem Leben eventuell nicht so viel Geld hat zuerst einen Testlauf durchzuführen. Allgemein kann man das Warteschlangenmodell in folgende Elemente aufteilen:

Kundenpopulation K – besagt wie viele Entitäten im System vorhanden sind. Bei den meisten Beispielen in der Vorlesung ist die Kundenpopulation unbeschränkt.
Ankunftsverteilung A – beschreibt wie schnell bzw. in welcher Art die Entitäten ankommen. Die Ankunftsverteilung kann durch verschiedene bereits bekannte Verteilungen beschrieben werden. Ein Beispiel wäre die Exponentialverteilung.
Warteschlange N – gibt die Länge der Warteschlange wieder. Die Größe der Warteschlange kann beschränkt werden. Kommt eine Entität bei vollen Warteschlange an geht diese verloren.
parallele Bedienstation c – Anzahl paralleler Bedienstationen.
Bedienzeitverteilung B – beschreibt wie die Entitäten an der Bedienstation bearbeitet werden. Die Bedienzeitverteilung kann man mit einer Verteilungsfunktion beschrieben werden. Ein Beispiel wäre die Normalverteilung.

Zur Unterscheidung der verschiedenen Warteschlangenmodelle nutzt man dann die Abkürzung A/B/c/N/K . Die Parameter A und B haben dabei folgende Wertebereiche:

M = exponentiell (markovian)
D = deterministisch (deterministic)
G = beliebig (general)

Hinweis: Ist die Warteschlangengröße und die Kundenpopulation unendlich groß, so lassen wir die letzten beiden Parameter weg: .

Wichtige Ergebnisse

Möchte man nun das Modell auswerten sind folgende Werte von besonderer Bedeutung:

– mittlere Ankunftsrate
– (mittlere) Bedienrate pro Station
– Streuung der Bedienrate

Ist die Ankunftsrate kleiner als die Bedienrate pro Station, können also die Entitäten schneller bearbeitet werden als diese ankommen, spricht man von Stationarität. Eine weitere Feststellung, die aus der Stationarität folgt ist, dass die Warteschlange nicht ins unendliche wächst. Weitere Größen sind:

– Gesamtzahl der Kunden im System zur Zeit
– stationäre Verteilung
– Erwartungswert von
– Langzeitausnutzung der Server
– Langzeitaufenthalt im System / Mittlere Aufenthaltszeit der Aufträge

Ziel der Warteschlangentheorie ist es dann die Verteilung von zu bestimmen. Ergebnisse für bestimmte Warteschlangen sind dann hier [1] zu finden. Zu guter letzt können wir festhalten, dass bei konstantem Erwartungswert und wachsender Streuung der Bedienzeit Warteschlangen länger werden. Außerdem tritt jede Warteschlangenlänge mit gewisser Wahrscheinlichkeit auf, d.h. Warteschlangen laufen stets gelegentlich voll und n Bedienstationen mit einer Warteschlange sind besser als n Bedienstationen mit n Warteschlangen.

Gesetz von Little

Das Gesetz von Little wird zur Konsistenzprüfung von Simulationsergebnissen verwendet. Es ist wichtig zu beachten, dass das Gesetz von Little auf alle stationären Warteschlangenmodelle angewendet werden kann. Es ist also unabhängig von der Ankunfts- und Bedienverteilung! Es besagt, die mittlere Anzahl der Aufträge entspricht dem Produkt von Eintreffrate und Aufenthaltszeit.

– mittlere Zahl der Aufträge im System
– mittlere Eintreffrate der Aufträge
– mittlere Aufenthaltszeit der Aufträge

Beispiel

Man betrachte das Wartenschlangenmodell der Tankstelle aus der Vorlesung. Man nehme an es kommen vier Kunden pro Minute mit exponentialverteilten Ankunftszeiten. Die Bezahlung dauert durchschnittlich 12 Sekunden und ist ebenfalls exponentialverteilt. Die einzige Möglichkeit zu bezahlen ist der Automat. Damit ergibt sich eine M/M/1 - Warteschlange. Die Formeln dazu findet man hier[1]. Die Bedingung für Stationarität wäre . Mit vier Kunden pro Minute wäre . Da das Bezahlen am Automaten im Durchschnitt 12 Sekunden dauert kommt man für auf . Es können pro Minute also ungefähr 5 Kunden an der Bedienstation bearbeitet werden. Damit gilt für diese Warteschlange Stationarität. Für die Langzeitausnutzung folgt . Wir haben also eine 80% Auslastung der Bedienstation. Der Erwartungswert der Anzahl der Kunden im System wäre dann und die Langzeitaufenthaltszeit beträgt .

Selbstest

Aussage in alter Prüfung: "Sowohl die Systemparameter als auch der Systemzustand eines Systemmodels ändern sich während eines Simulationslaufs." Ist diese Aussage richtig?
x ist eine kontinuierliche Größe (z.B., Aufenthaltszeit im Puffer). Für die Wahrscheinlichkeitsdichte f(x) gilt dann immer:
(1) , (2) , (3) , (4) ?
Aussage: "Bei Ereignissen, die negativ exponentiell verteilt sind, ist das Eintreffen des Ereignisses zu jedem Zeitpunkt gleichwahrscheinlich, unabhängig von der Zeit, die bisher vergangen ist." Ist diese Aussage richtig?
Das Gesetzt von Little setzt die mittlere Eintreffrate und die mittlere Aufenthaltszeit von Aufträgen mit der mittleren Zahl der Aufträge im System in Verbindung.
Die Wartezeit in einem Warteschlangenmodell nimmt zu, wenn σ bei konstantem μ wächst.
Eine M/M/3 Warteschlange hat…
Eine M/D/1/1/1 Warteschlangen hat...
Eine M/G/2/08/15 Warteschlangen hat…
Eine G/D/3 Warteschlangen hat...

(:antwortchecker:)

Links auf dieser Seite

[1] Warteschlangen

Feedback

Bei Fehlern oder Anregungen zu dieser Seite schicken Sie bitte eine Email an andrej.felde@stud.tu-darmstadt.de oder thomas.hesse@stud.tu-darmstadt.de.