Einführung in Computational Engineering – Vorlesung 7

Autoren: Andrej Felde und Thomas Hesse

Folien zur Vorlesung 7: Link
Folien zur Vorlesung 7 mit Annotationen: Link
Aufzeichnung der Vorlesung 7: Link
Übung 6: Link

Differentialgleichungslöser

Oft hat man es in der Praxis mit nichtlinearen Problemen zu tun. Hier wird nun versucht, eine effiziente Möglichkeit zu erarbeiten, mit der man die Gleichgewichtslösung einer nicht lineare Differentialgleichung bestimmen kann. Die Lösung dazu lautet "Differentialgleichungslöser". Mit den Differentialgleichungslösern versucht man im Allgemeinem stationäre Punkte oder eben nur einen stationären Punkt einer Differentialgleichung zu bestimmen. Dafür werden in der Regel Kontraktionen benutzt (selbst-abbildende Abbildungen). Im folgendem werden zwei Verfahren vorgestellt, welche den stationären Punkt (also die Gleichgewichtslage) einer Differentialgleichung bestimmen. Ein Beispiel für das zu bestimmende stationäre System sähe wie folgt aus:


Transiente Phase

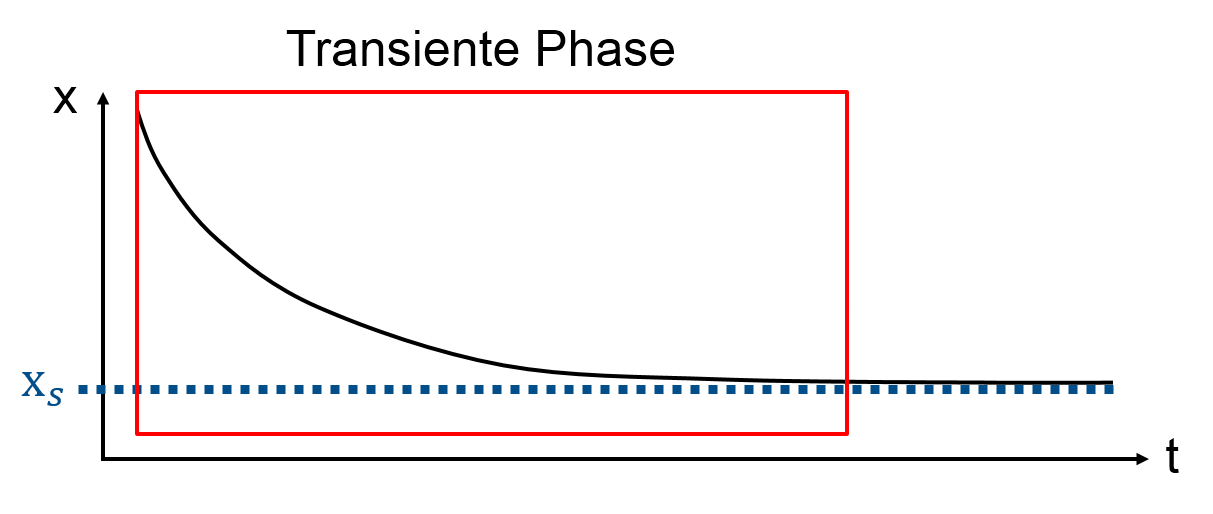
Die transiente Phase beschreibt genau den Zeitbereich, in dem das nicht lineare System sich nicht auf die Gleichgewichtslage einpendelt. Interessant ist demnach natürlich der Zustand des Systems nach der transienten Phase. Die Verfahren, welche zur Bestimmung der Gleichgewichtslage benutzt werden, versuchen gerade diese transiente Phase mit iterativen Ansätzen bis hin zur Gleichgewichtslösung zu durchlaufen.

Fixpunktiteration

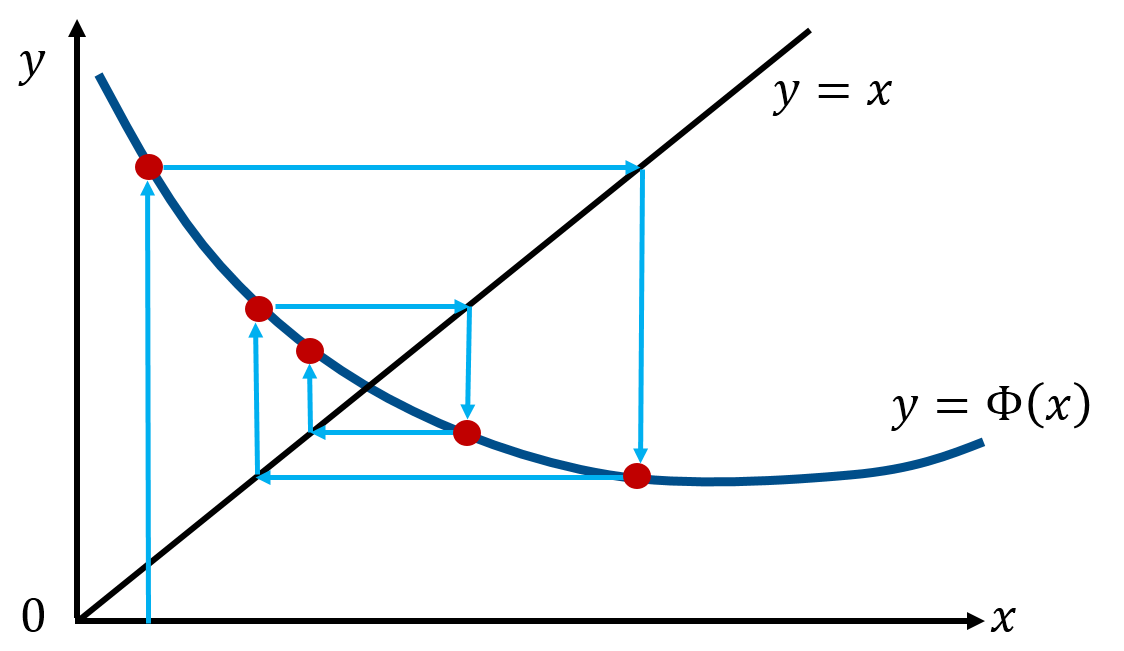
Allgemein handelt es sich bei der Fixpunktiteration um eine Abbildung, genauer eine Kontraktion. Eine Kontraktion ist eine Abbildung, die von sich wieder auf sich selbst abbildet, also eine selbst abbildende Abbildung. Für den Falle der Fixpunktiteration wird konkret von einem Banachraum nach einem Banachraum abgebildet. Ein Banachraum ist ein Vektorraum, auf dem eine Metrik (z.B. die euklidische Norm) definiert wurde und der vollständig ist. Das "vollständigkeits"-Kriterium ist genau dann erfüllt, wenn jeder Punkt des Raumes Cauchy-konvergent ist.
Die in der Vorlesung vorgestellte Form für die Fixpunktiteration einer nicht linearen Differentialgleichung wäre demnach mit der Kontraktion , da ja gerade gelten muss!

Beispiel

Man betrachte die Fixpunktiteration für die Kontraktion mit dem Startwert . Die ersten 5 Iterationen sind wie folgt:

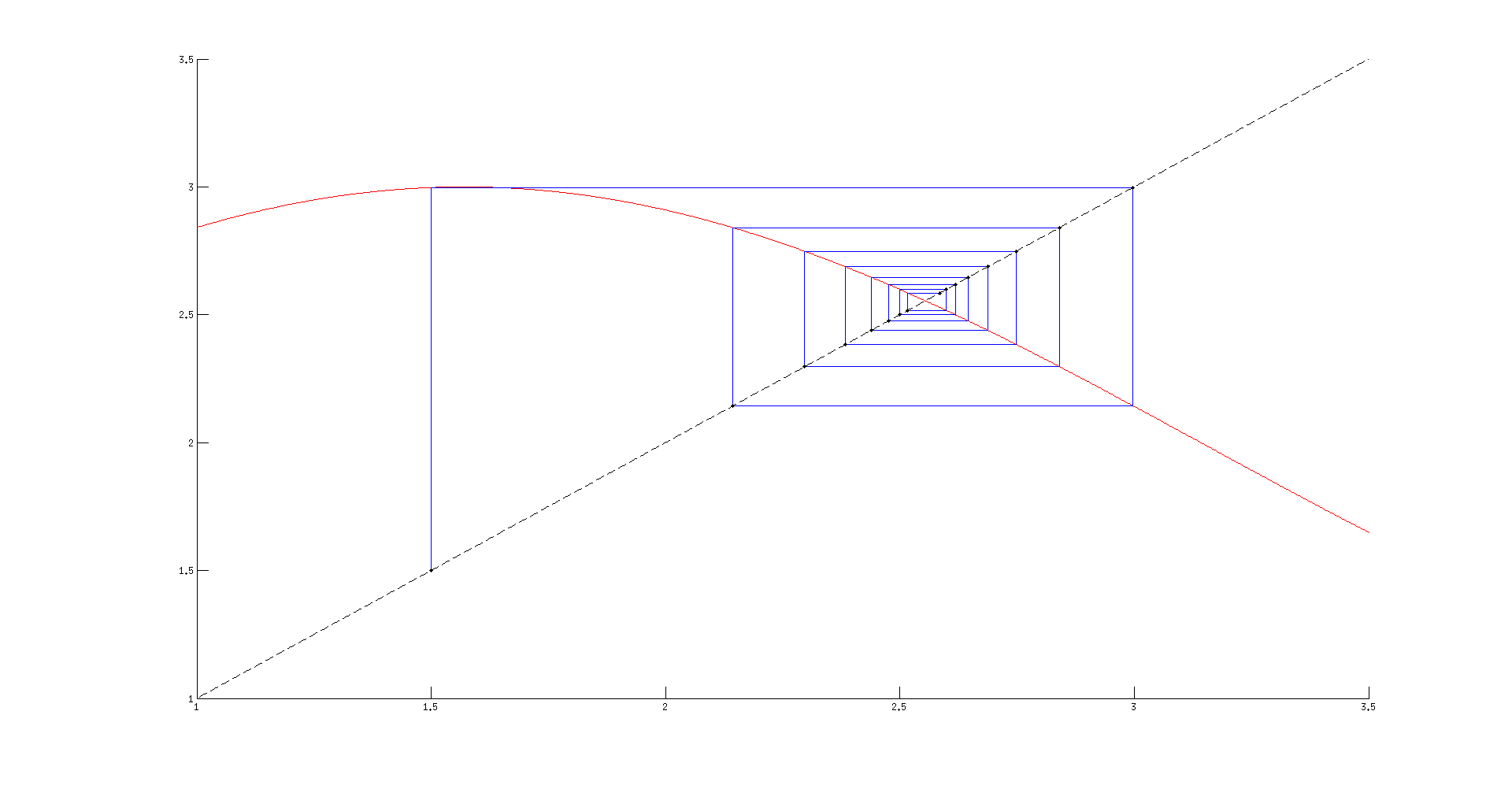
[...] Führt man nun dieses Verfahren weiter fort, so erhält man zum Schluss den Fixpunkt , welcher die Gleichgewichtslage an der ungefähren x-Position von ebenfalls ergibt. Das Bild der Fixpunktiteration mit den ersten 15 Iteration kann man sich hier noch einmal genauer anschauen.

Newton-Verfahren

Das Newton-Verfahren ist ein spezieller Fall der Fixpunktiteration genau dann, wenn die Folge gegen den Fixpunkt konvergiert. Das Newton-Verfahren wird ebenso wie die Linearisierung um die Gleichgewichtslage [1] mit dem Taylorpolynom ersten Grades hergeleitet, also bis zum linearen Term. Das Newton-Verfahren macht nichts anderes, als an bestimmten Funktionswerten zu linearisieren und den Wert an dem sich die x-Achse mit der Tangente schneidet als neuen Funktionswert zu verwenden. Hier zeichnet sich die iterative Vorgehensweise des Newton-Verfahrens ab. Die allgemeine Form der Newton Gleichung ist:

Ein Nachteil dieses Verfahrens ist die lokale Konvergenz. Durch die lokale Konvergenz kann es sein, dass das Verfahren zu große Schritte macht und deshalb divergiert. Das Newton-Verfahren wird solange ausgeführt, bis es terminiert. Die zwei Terminierungskritierien sind:

  1. Nahe der Lösung – in diesem Falle erreicht das Newton-Verfahren die Gleichgewichtslösung oder befindet sich in -Nähe zu der Gleichgewichtslösung
  2. Kein Fortschritt – festgelegte "Fortschrittsgrenze" wird zwischen den Iterationen unterschritten, ansonsten kann man ein Maximum an Iterationen festlegen


Beispiel

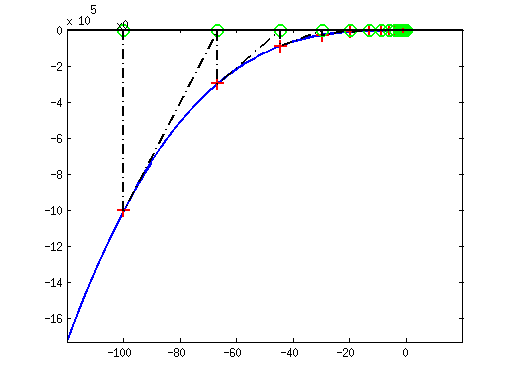
Also Beispiel wird hier das Newton-Verfahren angeführt bezüglich der Funktion . Hier wird versucht mit dem Startwert die Nullstelle der Funktion, bzw. des Polynoms, zu finden. Hier sieht man schön, wie an die Funktion von der die Nullstelle gesucht ist eine Tangente angelegt wird. Der Schnittpunkt der Tangente mit der x-Achse bildet den Eingangsparameter für die nächste Iteration des Newton-Verfahren. Dies wird dann so häufig wiederholt, bis das Newton-Verfahren konvergiert. Die Konvergenz ist erreicht, wenn z.B. nur noch sehr kleine Schritte gemacht werden und diese eine festgelegte Toleranz unterschreiten, also wobei z.B. .

Schrittweitensteuerung

Eine allgemeine Faustregel zur Wahl der Schrittweite ist, sie so "klein wie nötig und so groß wie möglich" zu wählen. Dabei ist die Schrittweite

so zu wählen, dass . Hierbei ist wünschenswert, da man damit quadratische Konvergenz für das Verfahren erreicht, es also schneller konvergiert.


Die Schrittweite liesse sich damit zum Beispiel mit bestimmen.

Selbstest

  1. Das System mit ist
  2. Für welches h ist das System mit stabil? Bitte die allgemeinste Lösung auswählen!
  3. Die Gleichgewichtslösung von ist...
  4. Das zeitkontinuierliche System mit wird als mit zeitdiskretisiert. Wie lautet der Zusammenhang zwischen A_1 und A_2?
  5. Das zeitkontinuierliche System von der vorherigen Frage ist stabil. Stimmt das auch für das zeitdiskrete System? Wenn ja, für welche Werte von ?
  6. Bestimme den Fixpunkt von mit . Welchen Wert hat er? (Tip: Taschenrechner haben COS Tasten…)
  7. Wir wollen mit Fixpunkt-Iteration in der Nähe von lösen. Was ist die Konvergenzbedingung? Eigenwerte von
  8. Wir wollen mit Fixpunkt-Iteration in der Nähe von lösen. Wie gross darf die Relaxation-"Matrix" höchstens sein?
  9. Das Newtonverfahren ist dem Fixpunktverfahren vorzuziehen falls...
  10. Die Wahl des Startvektors beim Newton-Verfahren kann das Berechnungsergebnis beeinflussen.

(:antwortchecker:)

Links auf dieser Seite

[1] Linearisierung um die Gleichgewichtslage

Feedback

Bei Fehlern oder Anregungen zu dieser Seite schicken Sie bitte eine Email an andrej.felde@stud.tu-darmstadt.de oder thomas.hesse@stud.tu-darmstadt.de.

  

zum Seitenanfang