(:requiretuid:)

Einführung in Computational Engineering – Vorlesung 4

Autoren: Andrej Felde und Thomas Hesse

Folien zur Vorlesung 4: Link
Folien zur Vorlesung 4 mit Annotationen: Link
Aufzeichnung der Vorlesung 4 mit Dozent: Link
Aufzeichnung der Vorlesung 4 ohne Dozent: Link
Übung 3: Link

Örtliche konzentrierte und verteilte Parameter

Wir wollen uns zuerst eine Intuition für die Begriffe des örtlich konzentrierten und verteilten Parameters verschaffen. Im allgemeinem verstehen wir diese Begrifflichkeiten als Differentialgleichungen. Den örtlich konzentrierten Parameter verstehen wir dabei als ein Differential von einem Parameter. Das bedeutet im Umkehrschluss, dass wir hierbei von gewöhnlichen Differentialgleichungen reden. Bei dem örtlich verteilten Parameter reden wir dann von partiellen Differentialgleichung. Dies lässt sich im Allgemeinem als eine Funktion mit mehreren Parametern betrachten. Beispiele dafür haben wir in der Vorlesung gesehen.

Jacobi Matrix

Bei der Jacobi Matrix handelt es sich um eine Methode Funktionen mehrerer Parameter zu differenzieren. Diese Methodik sollten sie schon in der Mathematik für Informatik 2 angeeignet haben. Wir wiederholen sie hier dennoch noch einmal kurz der Vollständigkeit wegen. Außerdem werden wir zeigen, wie man die Jacobi Matrix analytisch und numerisch herleitet.

Analytische Herleitung der Jacobi Matrix

Möchte man die Jacobi Matrix einer Funktion bestimmen, dann macht man dies mittels:

.


Numerische Herleitung der Jacobi Matrix

Die Jacobi Matrix kann auch numerisch über den Vorwärtsdifferenzenquotienten berechnet werden. Es gilt:

Dabei steht für den -ten Einheitsvektor, steht für die Schrittweite bezüglich des -ten Systemzustandes zusammen mit einer persönlich festgelegten Toleranzgrenze . Wir haben hierbei schon in der Vorlesung gesehen, wie man sich z.B. Werte wie wählen kann (dies ist nicht-trivial!). Des Weiteren wird in den Folien eine Intuition gegeben, wie diese Schrittweite zu verstehen ist.

Transformation einer Differentialgleichung (DGL)

Angenommen wir haben eine DGL n-ter Ordnung, dann können wir diese in ein DGL-System der Dimension n transformieren. Dafür führen wir den Systemzustand ein, wobei die i-te Komponente des Systemzustandvektors den ursprünglichen Systemzustand vom Grad i enthält. Wir betrachten dieses Vorgehen an folgendem Sachverhalt:
Angenommen wir haben ein DGL System zweiter Ordnung von der Form . Als erstes substituieren wir die Systemzustände. Sei und . Diese bilden dann den Vektor . Dann können wir auch schon das DGL System aufstellen! Es ergibt sich:

Damit haben wir dann eine DGL zweiter Ordnung auf ein DGL System erster Ordnung transformiert.

Autonomisierung einer Differentialgleichung (DGL)

Bei der Autonomisierung von Differentialgleichungen geht es lediglich darum, die Differentialgleichung nicht mehr explizit von der Zeit abhängig zu machen. Dies hat den Vorteil, dass das System dann nur noch von Systemzuständen abhängt und nicht mehr von einer zeitlichen Komponente.

Lineare und nicht-lineare Systeme

Bei Differentialgleichungen können zwischen linearen und nicht-linearen Systemen differenziert werden.

Lineare Systeme

Bei linearen Systemen handelt es sich meist um sehr einfache Differentialgleichungen der Form vereinfacht dargestellt. Hierbei handelt es sich bei der Matrix um die Systemmatrix und bei um die Zustandsmatrix. Lineare Systeme kann man sich wie eine Funktion vorstellen, wobei die darstellende Matrix der Funktion wäre.

Nicht-lineare Systeme

Nicht-lineare Systeme sind im Gegensatz zu den linearen Systemen meist sehr komplexe Differentialgleichungen der Form vereinfacht dargestellt. Bei der Funktion handelt es sich dabei um eine nicht-lineare Funktion. Diese können sich z.B. aus verschiedenen interpolierten Polynomen zusammensetzen oder gar Splines sein. Für solche Problemstellung stellt die Mathematik zudem nicht so viele Rechenregeln zur Verfügung. Oft ist der Ansatz, dass man nicht-lineare Systeme einfach in lineare Systeme überführt. Dafür benutzen wir die Linearisierung in einem Punkt.

Existenz einer Lösung zu einer Differentialgleichung (DGL)

Die Lösung einer linearen Differentialgleichung existiert genau dann, wenn wir eine reguläre Systemmatrix vorliegen haben. Das heißt, dass die Matrix insbesondere invertierbar ist und damit auch vollen Rang hat. Die Existenz einer Lösung von einer nicht-linearen Differentialgleichung lässt sich so z.B. nachweisen mit dem Satz von Picard-Lindelöf, welcher uns dann auch später zur Fixpunkt Iteration (kurz: FPI) führt! Eine weitere Alternative zur Feststellung der Existenz einer Lösung zu einer nicht-linearen Differentialgleichung bietet der Satz von Peano.

Linearisierung um Gleichgewichtslage / Gleichgewichtspunkt

Bei der Linearisierung um einen Punkt handelt es sich im allgemeinem um eine tangentiale Approximation an eine nicht-lineare Funktion mit einer linearen Funktion, wobei nur dieser eine Punkt exakt dargestellt ist. Man berechnet diese wie folgt:

  1. Bestimmung der allgemeinen Jacobi Matrix der nicht-linearen Funktion , sodass man erhält.
  2. Einsetzen des Punktes / Gleichgewichtspunktes um den linearisiert werden soll, also .
  3. Dann lässt sich die linearisierte Funktion um diesen Punkt mit aufstellen. Diese Betrachtung folgt aus der Herleitung durch die Taylorreihe oder des Taylorpolynoms für eine gewisse -Genauigkeit.

Natürlich ist dieser Vorgang nur für Punkte zulässig, ist aber genau so wie er dort steht auf ein anders-dimensionales Beispiel zu übertragen.

Stabilitätsbetrachtung von Systemen

Bei der Stabilitätsbetrachtung von Systemen setzen wir die Berechnung von Eigenwerte voraus. Ein möglicher analytischer Ansatz zum Berechnen von Eigenwerten wäre demnach zum Beispiel mithilfe des charakteristischen Polynoms mit Systemmatrix . Nun wollen wir im folgenden anhand der Eigenwerte eines Systems die Stabilität im reellen, sowie im imaginären bestimmen können. Systeme, bei denen sich die Eigenwerte im imaginärem Bereich bewegen, basieren meistens auf Amplituden und Schwingungen.
Wir betrachten im folgendem die Fälle von Stabilität und Instabilität für reelle Eigenwerte:

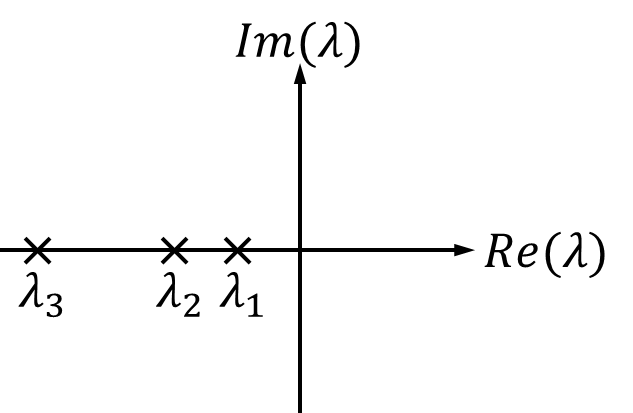
  • Die Eigenwerte sind hier wie gesagt alle reell und alle kleiner null. Damit ist diese Grafik ein Beispiel für ein stabiles System.


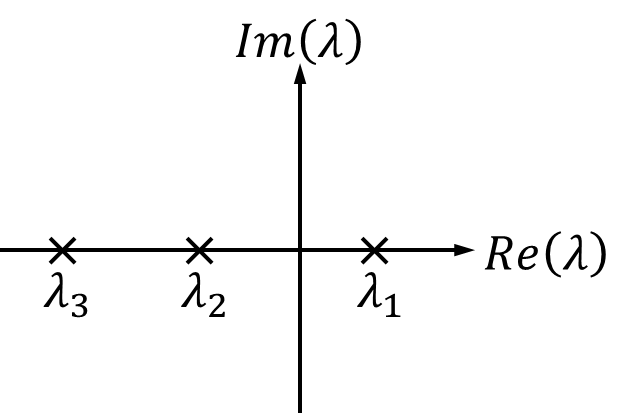
  • Die Eigenwerte bei diesem System sind nicht alle kleiner null. Damit ist das System im Gesamten instabil.


Nun betrachten wir Stabilität und Instabilität für komplexe Eigenwerte:

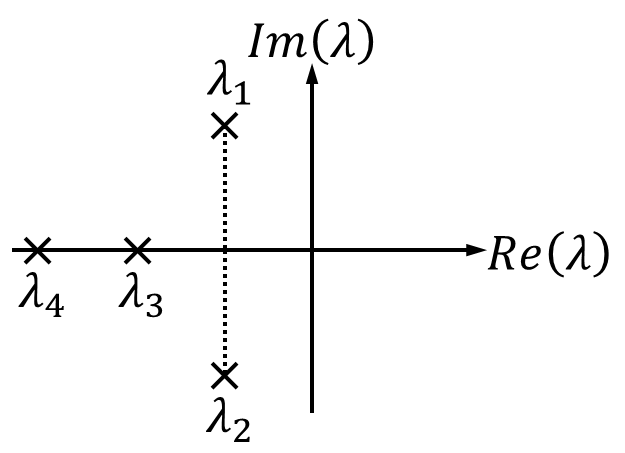
  • Die Eigenwerte sind hier wie gesagt alle komplex und im Realteil alle kleiner null. Damit ist diese Grafik ein Beispiel für ein stabiles System.


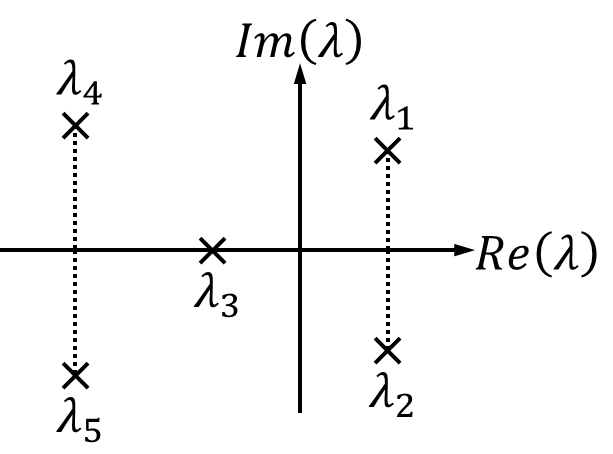
  • Die Eigenwerte bei diesem System sind für den Realteil einiger Eigenwerte nicht kleiner null. Damit ist das System im Gesamten instabil.


Beispiel

In dem YouTube-Video sehen wir zum Beispiel ein inverses Pendel. Hierbei ist die Gleichgewichtslage genau dort, wo das Pendel gerade nach oben oder unten steht und weder nach links, noch rechts kippt. Die untere Gleichgewichtslage ist dabei stabil und die obere ist instabil. Diese Betrachtung nehmen wir in den Vorlesungsfolien 5 genauer vor.

Selbstest

  1. Ein linearer Kongruenz-Generator erzeugt KEINE ...
  2. Das Gesetz von Little sagt zu Systemen mit stationären Zustand NICHT vorher dass die mittlere Schlangenlänge...
  3. Eine Differentialgleichung enthält immer Ableitungen von Variablen…
  4. Der menschliche Gang läßt sich gut modellieren mit …
  5. Das Schwingen von Seilen im Wind läßt sich gut Modellieren mit ...
  6. Jedes dynamische System besitzt einen Gleichgewichtspunkt.
  7. Ein autonomes DGL System 1. Ordnung hat eine eindeutige Lösung:
  8. Numerische Berechnung von Jacobimatrizen ist …
  9. Die Gleichgewichtslage heißt dann stabil, wenn eine durch eine kurz andauernde und nicht zu große Störung verursachte Abweichung aus dieser Lage im Laufe der Zeit gegen Null strebt.
  10. Jedes System kann linearisiert werden!

(:antwortchecker:)

Feedback

Bei Fehlern oder Anregungen zu dieser Seite schicken Sie bitte eine Email an andrej.felde@stud.tu-darmstadt.de oder thomas.hesse@stud.tu-darmstadt.de.

  

zum Seitenanfang