(:requiretuid:)

Einführung in TGDI – Kapitel 5

Autoren: Anna Wenzelburger, Moritz Fischer, Patrick Meyn

Arithmetische Schaltungen

Einleitung

Die Grundelemente digitaler Schlatungen sind: Gatter, Multiplexer, Decoder, Register, Arithmetische Schaltungen, Zähler, Speicher und programmierbare Logikfelder.

Diese veranschaulicht man durch:

Diese Grundelemente werden für den Aufbau eines eigenen Mikroprozessors verwendet (dazu in Kapitel 7 mehr)

1 - Bit Addierer

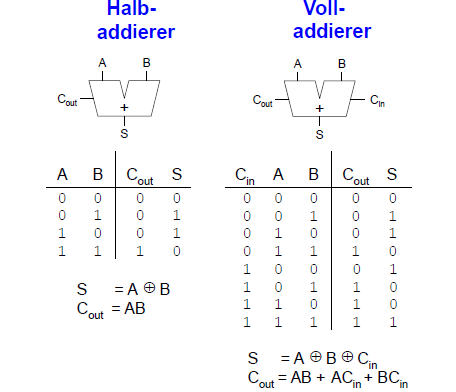
Mehrbit-Addierer mit Weitergabe von Übergängen

Diese werden auch Carry-propagate adder (CPA) genannt. Dabei gibt es verschiedene Typen:

• Ripple-carry-Addierer (langsam)
• Carry-Lookahead Addierer (schnell)
• Prefix-Addierer (noch schneller)

Der Carry-Lookahead und Prefix-Addierer sind schneller bei breiteren Datenworten, benötigen dafür aber auch mehr Fläche.

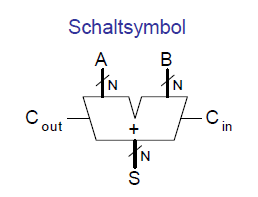
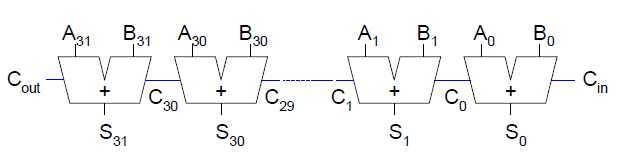
Ripple-Carry-Addierer

Der Ripple-Carry-Addierer besteht aus einer Kette von 1-bit-Addierern. Die Überträge werden von niedrigen zu hohen Bits weitergegeben. Sie ripplen sich durch die Schaltung.

Dadurch ist der Ripple-Carry-Addierer langsam.

Die Verzögerung durch einen N-bit Ripple-Carry-Addierer berechnet sich durch

dabei ist die Verzögerung durch einen Volladdierer.

Carry-Lookahead-Addierer (CLA)

Statt Bit-zu-Bit Einzelberechnungen, wird nun der Carry jeweils für Blöcke von k-Bits berechnet. Dazu werden 2 Signale eingeführt:

• Generate: Erzeuge einen Übertrag
• Propagate: Leite einen eventuellen Übertrag weiter

Wie vorher beim Ripple-Carry-Addierer werden die Bits in Spalten organisiert, jetzt gibt es aber mehrere Zeilen.

Definitionen

Eine Spalte (Bit i) produziert einen Übertrag an ihrem Ausgang C_i

• Wenn sie den Übertrag selbst erzeugt (Generate, G_i)
• Wenn sie einen von C_i-1 eingehenden Übertrag weiterleitet (Propagate, P_i)

Eine Spalte (Bit i) erzeugt einen Übertrag falls A_i und B_i beide 1 sind.

Eine Spalte (Bit i) leitet einen eingehenden Übertrag weiter falls A_i oder B_i 1 ist.

Damit ist der Übertrag C_i aus der Spalte i heraus:

Carry-Lookahead-Verfahren

1. Berechne G und P Signale für einzelne Spalten (Einzelbits)
2. Berechne G und P Signale für Gruppen von k Spalten (k-Bits)
3. Leite C_in nun nicht einzelbitweise, sondern in k-Bit Sprüngen weiter (Jeweils durch einen k-bit Propagate/Generate-Block).

Als Beispiel wollen wir dieses Verfahren nun an einem 4b Block (CLA für 2 4b Zahlen) durchgehen. Dazu müssen wir die Signale P_3:0 und G_3:0 bestimmen.

Wir überlegen uns zunächst, wann ein ein 4b Block einen Übertrag erzeugt. Dies ist der Fall, wenn:

• Spalte 3 einen Übertrag erzeugt (G₃ = 1) oder
• Spalte 3 einen Übertrag weiterleitet (P₃ = 1), der vorher erzeugt wurde

Der 4b Block leitet einen Übertrag direkt weiter, wenn alle Spalten den Übertrag weiterleiten.

Damit ist der Übertrag durch einen i:j Bit breiten Block C_i

32-bit CLA mit 4b Blöcken

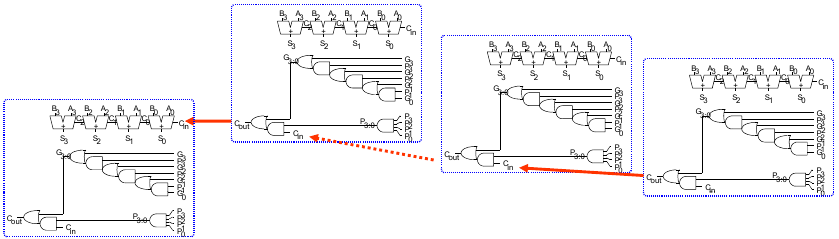
Wir können die 4b Blöcke nun verwenden, um aus ihnen einen breiteren CLA zusammenzusetzen. Zum Beispiel verwenden wir acht Stück, um einen 32-bit CLA zu konstruieren.

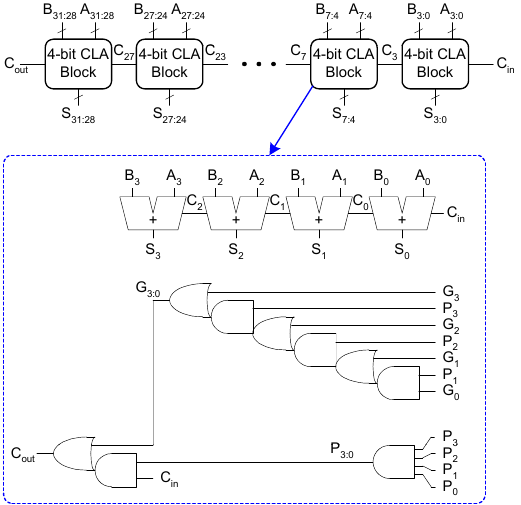
Dabei gilt G_i = A_i B_i und P_i = A_i + B_i. Wir schließen also immer den C_out eines 4b Blocks an den C_in des darauffolgenden Blockes an.

Verzögerung

Die Verzögerung durch einen N-bit CLA mit k-bit Blöcken berechnet sich nach

wobei

• t_pg : Verzögerung P, G Berechnung für eine Spalte (ganz rechts)
• t_pgBlock : Verzögerung P, G Berechnung für einen Block (rechts)
• t_AND/OR : Verzögerung durch AND/OR je k-Bit CLA Block (“Weiche”)
• kt_FA : Verzögerung zur Berechnung der k höchstwertigen Summenbits

Für N > 16 ist ein CLA oftmals schneller als ein Ripple-Carry-Addierer. Aber die Verzögerung hängt immer noch von N ab und ist im wesentlichen linear.

Präfix-Addierer

Der Präfix-Addierer führt die Ideen des CLA weiter. Er berechnet den Übertrag C_i-1 in jede Spalte i so schnell wie möglich. Dabei berechnet sich die Summe jeder Spalte folgendermaßen.

Um alle C_i schnell zu berechnen, berechnet ein Präfix-Addierer P und G für größer werdende Blöcke. Also Blöcke der Größe 1b, 2b, 4b, 8b usw. Solange bis die Eingangsüberträge für alle Spalten bereitstehen.
Dadurch besteht der Präfix-Addierer nicht mehr aus N/k Stufen, sondern nur noch log₂N Stufen. Die Breite der Operanden geht also nur noch logarithmisch in die Verzögerung ein.
Der Preis für die geringe Verzögerung ist, dass für einen Präfix-Addierer sehr viel Hardware erforderlich ist.

Bei einem Präfix-Addierer wird ein Übertrag...

• entweder in einer Spalte i generiert
• oder aus einer Vorgängerspalte i-1 propagiert

Definition: Der Eingangsübertrag C_in in den ganzen Addierer kommt aus Spalte -1

Der Eingangsübertrag in eine Spalte i ist der Ausgangsübertrag C_i-1 der Spalte i-1

G_i-1:-1 ist das Generate-Signal von Spalte -1 bis Spalte i-1

Interpretation: Ein Ausgangsübertrag aus Spalte i-1 entsteht...

• wenn der Block i-1:-1 selbst einen Übertrag in i-1 generiert
• oder aus i-2, i-3 usw. weiterleitet

Damit ist die Summenformel für die Spalte i umschreibbar zu

Deshalb ist nun das Ziel der Hardware-Realisierung, so schnell wie möglich G_0:-1, G_1:-1, G_2:-1, G_3:-1, G_4:-1, G_5:-1 usw. zu bestimmen. Die sogenannten Präfixe.

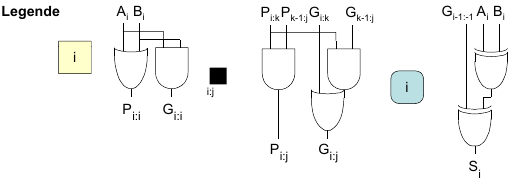
Die Berechnung von P und G für einen variabel großen Block funktioniert folgendermaßen.

Es gelte:

• Höchstwertiges Bit: i
• Niederwertiges Bit: j
• Unterteilt in zwei Teilblöcke (i:k) und (k-1:j)

So ergibt sich für einen Block i:j

Bedeutung:

Ein Block erzeugt einen Ausgabeübertrag, falls

• in seinem oberen Teil (i:k) ein Übertrag erzeugt wird oder
• der obere Teil einen Übertrag weiterleitet, der im unteren Teil (k-1:j) erzeugt wurde.

Ein Block leitet einen Eingabeübertrag als Ausgabeübertrag weiter, falls sowohl der untere als auch der obere Teil den Übertrag weiterleiten.

Aufbau eines Präfix-Addierers

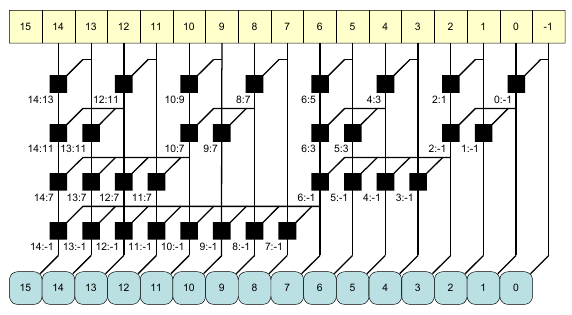
Verzögerung durch einen Präfix-Addierer

wobei

• t_pg : Verzögerung durch P, G-Berechnung für Spalte i (ein AND bzw. OR-Gatter)
• t_pg-prefix : Verzögerung durch eine Präfix-Stufe (AND-OR Gatter)
• t_XOR : Verzögerung durch letztes XOR der Summenberechnung

Vergleich von Addiererverzögerungen

Als Beispiel berechnen wir hier die Verzögerung bei einer 32b Addition mit einem Ripple-Carry, einem Carry-Lookahead (4-bit Blöcke) und einem Präfix-Addierer. Dabei haben die Volladdierer eine Verzögerung von t_FA = 300 ps und die Zwei-Eingangs Gatter eine Verzögerung von t_AND = t_OR = t_XOR = 100ps.

Subtrahierer

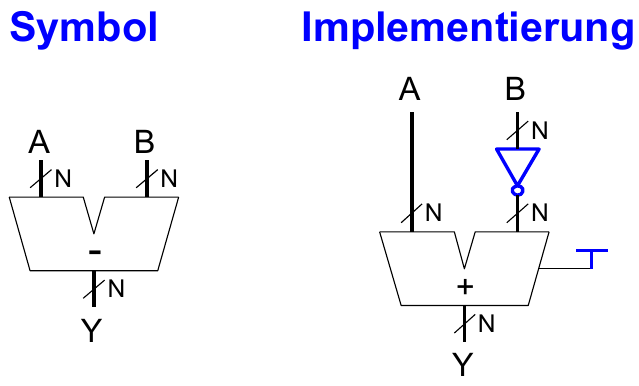
Vergleicher: Gleichheit

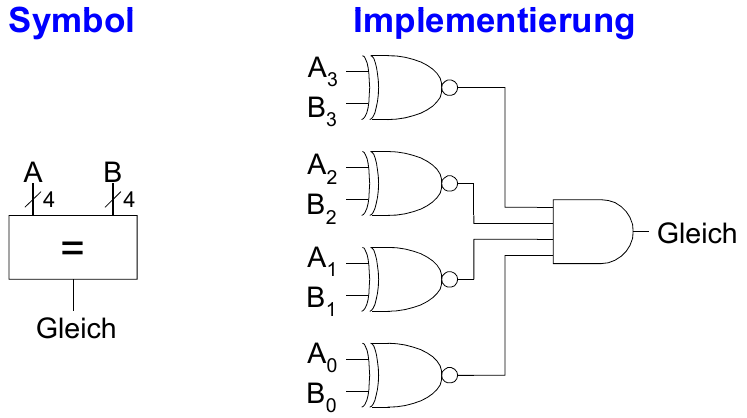
Vergleicher: Kleiner-Als

Für vorzeichenlose Zahlen

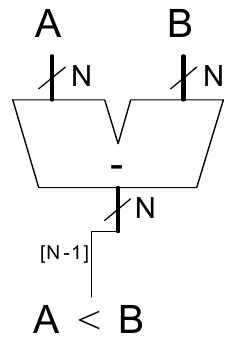
Arithmetisch-logische Einheit (arithmetic logic unit, ALU)

Schaltsymbol

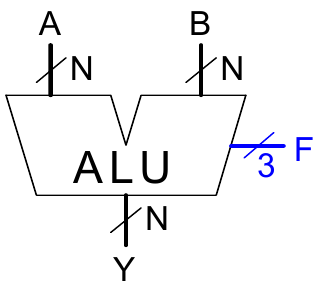
Tabelle der ALU-Operationcodes

Schaltplan

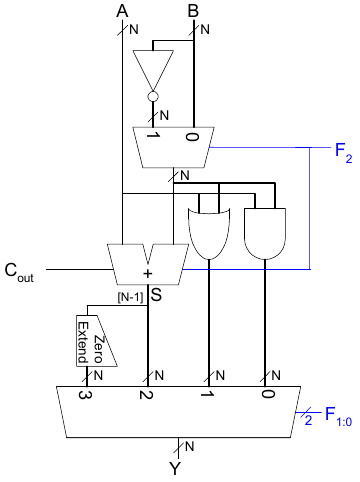
Beispiel: Set Less Than (SLT)

In diesem Beispiel konfigurieren wir die 32b ALU für eine SLT-Berechnung. Wir nehmen dabei an, dass A = 25 und B = 32 ist. Als Ausgabe erwarten wir A < B, also Y = 32'b1. Wir setzen den Steuereingang entsprechend der Tabelle für SLT: F_2:0 = 3'b111. Aus dem Schaltplan wird dabei ersichtlich, dass das Signal F₂ = 1'b1 den Addierer als Subtrahierer konfiguriert. Somit ergibt sich für das Signal S = A - B = 25 - 32 = -7. Da der Wert von S im Zweierkomplement vorliegt, also S = -7 = 32'h0xfffffff9, ist, das msb von S, S₃₁ = 1. Mit F_1:0 = 2'b11 wählen wir Y = S₃₁ mit einem Zero Extend als Ausgabe. Insgesamt ergibt sich Y = S₃₁ (zero extend) = 32'h00000001.

Schiebeoperationen (shifter)

Logisches Schieben

Der Wert wird um eine Bitposition verschoben. Leere Stellen werden mit 0 aufgefüllt.

Beispiele:

• 11001 >> 2 = 00110
• 11001 << 2 = 00100

Arithmetisches Schieben

Der Wert wird, wie beim logischen Schieben, um eine Bitposition verschoben. Beim Rechtsschieben wird jedoch der alte Wert des msb zum Auffüllen leerer Stellen verwendet.

Beispiele:

• 11001 >>> 2 = 11110
• 11001 <<< 2 = 00100

Rotierer

Hierbei werden Bits im Kreis rotiert, d.h. herausgeschobene Bits tauchen am anderen Ende wieder auf.

Beispiele:

• 11001 ROR 2 = 01110
• 11001 ROL 2 = 00111

Aufbau von Shiftern

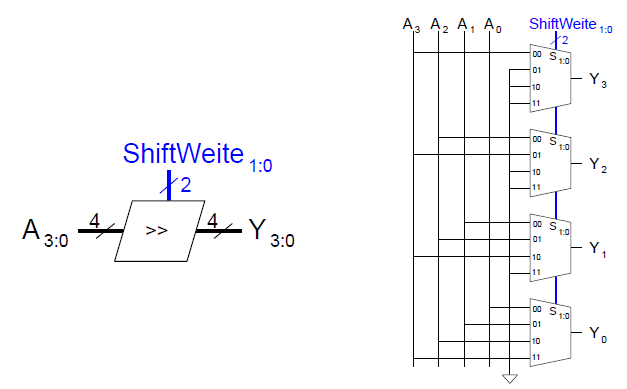
Shifter als Multiplizierer und Dividierer

Logisches Schieben um N Stellen nach links multipliziert den Zahlenwert mit

• Beispiel: 00001 << 2 = 00100
• Beispiel: 11101 << 2 = 10100

Arithmetisches Schieben um N Stellen nach rechts dividiert den Zahlenwert durch

• Beispiel: 01000 >>> 2 = 00010
• Beispiel: 10000 >>> 2 = 11100

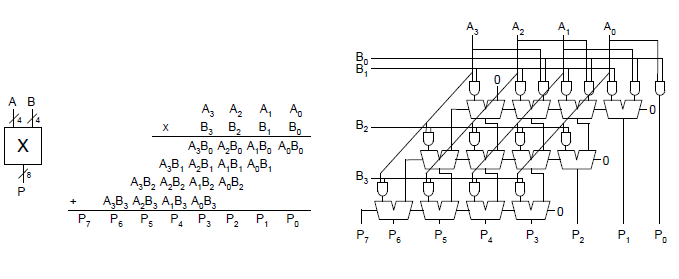
Multiplizierer

Schrittweise Multiplikation in Dezimal- und Binärdarstellung:

• Das Multiplizieren des Multiplikanden mit einer einzelner Stelle des Multiplikators berechnet ein Teilprodukt. Dies wird auch partielles Produkt genannt.
• Die entsprechend der Wertigkeit der aktuellen Multiplikatorstelle nach links verschobenen partiellen Produkte werden aufaddiert.

4 4 Multiplikator

Division

Sobald die Division einfach dargestellt wird, wird sie leider sehr langsam. Demnach wird sie etwas schneller, wenn sie kompliziert wird. Die Division ist aber immer deutlich langsamer als z.B. die Multiplikation.

Deshalb ist sie für eine Einführungsverantstaltung eher ungeeignet, die Beschreibung im Buch ist auch leider ziemlich schlecht... Deswegen wird die Division hier nur gestreift.

Idee: Quotient ziffernweise bestimmen

Notation

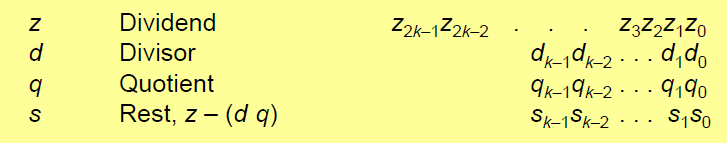
Dividiere vorzeichenlose Zahlen:

Dividend z (2k Bit breit) durch Divisor d (k Bit breit)

Ergebnis:

Quotient q (k Bit breit) und Rest s (k Bit breit)

Es gilt: z = q d + s

Auftreten von Überläufen

Beispiel: k=8, ergo 16b Dividend, 8b Divisor, 8b Quotient, 8b Rest.

Problem: nicht alle Ergebnisse sind repräsentierbar!

Operanden: z = 65534, d = 2

Ergebnis: q = 32767 ist nicht mehr in 8b darstellbar, Überlauf! s = 0

Vorgehensweise: Vorher auf darstellbares Ergebnis prüfen

• Vermeidet Überlauf
• Fängt Division durch 0 ab

Maximalwert für Dividenden:

• Maximalwert für q (k Bit breit):
• Maximalwert für s (k Bit breit):
• Es gilt:

Damit ergibt sich :

impliziert: Wenn , dann kein Überlauf

Generelles Vorgehen bei Division

Hier ein einfaches (aber langsames) Vorgehen:

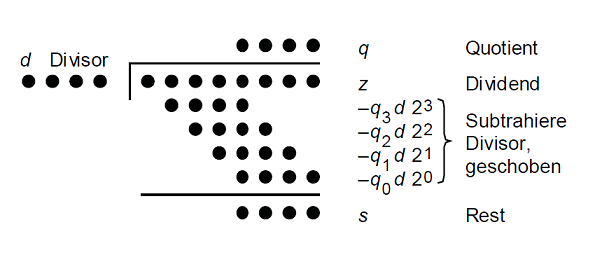
Optimierung: Schiebe nicht Divisor nach rechts sondern partiellen Rest nach links

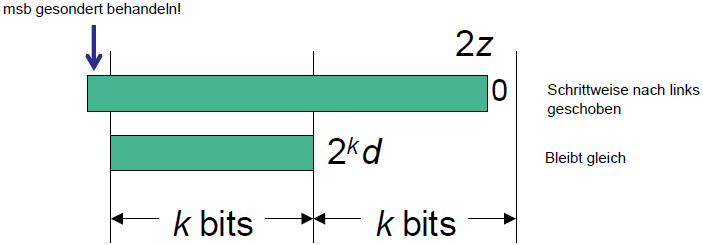
Algorithmus für 2k Bit Dividend / k Bit Divisor

• Schritt 0: Initialisiere partiellen Rest mit Dividend
• Schritt j: Schiebe partiellen Rest um ein Bit nach links und subtrahiere versuchsweise um k-Bit verschobenen Divisor.

Falls Differenz >= 0: , sonst

• Schritt k: Ende

Beispiel 8b Dividend, 4b Divisor: 117 / 10

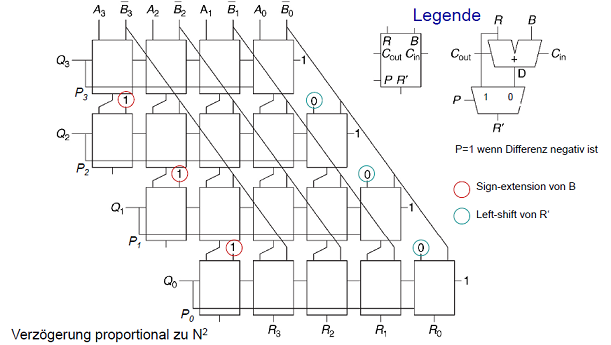
Kombinatorischer 4 x 4 Array Dividierer: A / B

Zahlensysteme

Wir haben bisher verscheidene Zahlensysteme kennen gelernt:

• positive Zahlen

• negative Zahlen

Es fehlen also noch Brüche, rationale Zahlen und reelle Zahlen.

Zahlen mit Bruchanteilen

Es gibt zwei gängige Darstellungen:

• Festkomma (fixed-point):

Die Position des Kommas bleibt konstant.

Beispiel: Dezimalsystem, 2 Vorkomma-, 3 Nachkommastellen

nicht: 3,1415 365,250

• Gleitkomma (floating-point):

Die Position des Kommas kann wandern, ist stets rechts der höchstwertigen Stelle <>0. Die Position des Kommas wird durch die Exponentenschreibweise angegeben.

Beispiele: Dezimalsystem, insgesamt 5 Stellen

nicht:

Es gibt eine Obergrenze für Exponenten. Man kann keine beliebig großen Zahlen darstellen.

Binäre Festkommazahlen

Die Darstellung von 6,75 mit 4b für den ganzen Anteil und 4b für den Binärbruch:

0110110 -> 0110 , 1100

Das Binärkomma wird nicht explizit dargestellt. Die Position wird durch das Format impliziert (hier: 4,4).

Dies hat den Nachteil, dass alle Leser und Schreiber von Festkommadaten das selbe Format verwenden müssen.

in 8b im binären 4,4 - Festkommaformat: 0111 1000

Vorzeichenbehaftete Festkommazahlen

Wie bei ganzen Zahlen sind auch hier zwei Darstellungen möglich. Auch hier gibt es die Vorzeichen-/Betragsform und das Zweierkomplement.

in 8b im binären 4,4 - Festkommaformat Vorzeichen/Betrag: 11111000 in 8b im binären 4,4 - Festkommaformat Zweierkomplement: +7,5 = 0111 1000, invertiert: 1000 0111, +1 -> 1000 1000

Binäre Gleitkommazahlen

Das Binärkomma liegt immer genau rechts von der höchswertigen 1. Dies ist ähnlich zur wissenschaftlichen Darstellung von Dezimalbrüchen. Die 4,387263 in wissenschaftlicher Darstellung ist .

Die Allgemeine Schreibweise ist:

dabei ist:

• M = Mantisse
• B = Basis
• E = Exponent

Im Beispiel haben wir hier: M = 4,387263, B = 10 und E = 6

Binäre Gleitkommazahlen

Beispiel: Stelle den Wert 288 als 32b-Gleitkommazahl dar.

Wir stellen hier drei Versionen dar, dabei ist aber nur die letzte davon eine Standarddarstellung!

1. Versuch

Wandle die Dezimalzahl in die Binärdarstellung um:

Trage nun die Daten in die Felder des 32b Wortes ein:

• Das Vorzeichenbit ist positiv (0)
• Die 8b des Exponenten stellen den Wert 7 dar
• Die verbliebenen 32 Bit stellen die Mantisse dar

2. Versuch

Wir beobachten, dass das erste Bit der Mantisse immer eine 1 ist.

Man kann sich das explizite Abspeichern der führenden 1 also sparen, da sie immer implizit als präsent angenommen wird.

Stattdessen speichert man nur den Bruchanteil (die "Nachkommastellen") explizit ab.

3. Versuch

Der Exponent kann auch negativ sein. Hier ist aber die Idee des Zweierkomplements möglich, sie hat aber praktische Nachteile. Besser ist es den Exponent relativ zu einem konstanten Grundwert (Exzess, Biaswert) anzugeben.

Hier ist der Biaswert = 127 (0111 1111)

Der Exponent mit Bias = Biaswert + Exponent
Der Exponent 7 wird also gespeichert als:

Damit hat man die IEEE 754 32-bit Gleitkommadarstellung von 288

Beispiel IEEE 754 Gleitkommadarstellung

Wir stellen hier -58,25 gemäß dem IEEE 754 32-bit Gleitkommastandard dar.

1. Wir wandeln in die Binärdarstellung um:

2. Wir tragen die Felder des 32b Gleitkommawortes ein:

• Vorzeichen: 1 (negativ)
• 8 Bits für Exponenten: (127 + 5) = 132 = 1000 0100
• 23 Bits für den Bruchanteil: 110 1001 0000 0000 0000 0000

In Hexadezimalschreibweise ist dies 0xC2690000.

IEEE 754 Gleitkommadarstellung: Sonderfälle

Nicht alle benötigten Werte sind nach dem Schema darstellbar.

Zum Beispiel hat die 0 keine führende 1.

Genauigkeit der Gleitkommadarstellungen

• Einfache Genauigkeit (single-precision):

• Doppelte Genauigkeit (double-precision)

Rundungsmodi für Gleitkommazahlen

• Overflow: Der Betrag der Zahl ist zu groß, um korrekt dargestellt zu werden
• Underflow: Die Zahl ist zu nahe bei 0, um korrekt dargestellt zu werden
• Rundungsmodi:

Beispiel: Runde 1,100101 (1,578125) auf 3 Bits Bruchanteil

• Ab: -> 1,100
• Auf: -> 1,101
• Zu Null: -> 1,100
• Zu nächster: -> 1,101 (1,625 liegt näher an 1,578125 als an 1,5)

Addition von Gleitkommazahlen mit gleichem Vorzeichen

1. Exponenten- und Bruchanteilfelder aus Gleitkommawort extrahieren

2. Bruchanteil um die führende 1 erweitern, um die Mantisse zu bilden

3. Vergleiche den Exponenten

4. Schiebe die Mantisse von der Zahl mit dem kleineren Exponenten nach rechts (bis die Exponenten gleich sind)

5. Addiere die Mantissen

6. Normalisiere die Mantissen und passe den Exponenten falls nötig an

7. Runde das Ergebnis entsprechend dem gewählten Rundungsmodus

8. Baue das Gleitkommawort aus Exponenten und Bruchanteil des Ergebnisses

Beispiel: Addition von Gleitkommazahlen

Wir addieren hier die beiden Gleitkommazahlen 0x3fC00000 und 0x40500000.

1. Extrahiere den Exponenten und den Bruchanteil aus 32b Worten

2. Erweitere den Bruchanteil um die führende 1, um die Mantisse zu bilden

M1: 1,1 M2: 1,101

3. Vergleiche die Exponenten

E2 - E1 = 128 -127 = 1, N1 muss also um ein Bit geschoben werden.

4. Die Mantisse der Zahl mit dem kleineren Exponenten entsprechend nach recht schieben

M1: 1,1 >> 0,11

5. Mantissen addieren (haben jetzt den gleichen Exponenten)

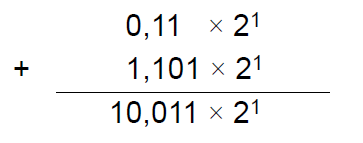
6. Normalisiere die Mantisse und passe den Exponenten an, falls nötig

7. Runde das Ergebnis entsprechend dem Rundungsmodus

Dies ist hier nicht nötig, da unser Ergebnis in 23Bit passt.

8. Baue aus Exponent und Mantisse ein neues Gleitkommawort für das Ergebnis

S = 0
E = 2 + 127 = 129 = 1000 0001
F = 001 1000 ... 0000

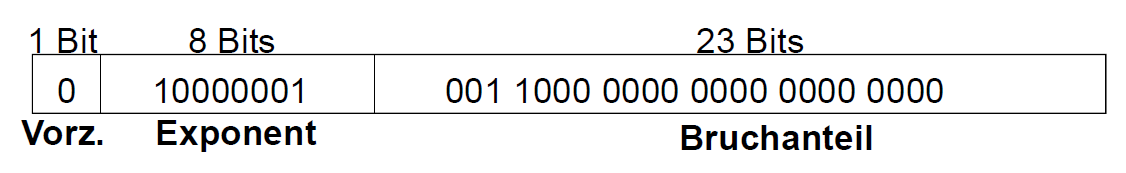
Das Ergebnis in Hexadezimalschreibweise ist 0x40980000.

Zähler

Im einfachsten Fall wird ein Zähler zu jeder positiven Taktflanke inkrementiert. Es wird durch einen Zyklus von Werten gezählt. Zum Beispiel bei 3b Breite: 000, 001, 010, 011, 100, 101, 110, 111, 000, 001,...
Beispielanwendungen sind Digitaluhren oder ein Programmzähler (zeigt auf die nächste auszuführende Instruktion).

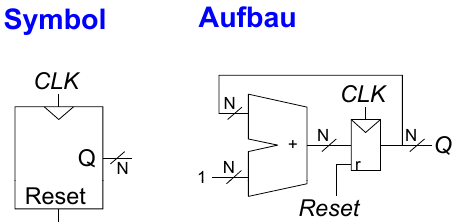
Schieberegister

Bei einem Schieberegister (auch: FIFO, first-in first-out) wird jeden Takt ein neuer Wert eingeschoben und ein alter Wert ausgeschoben. Dadurch kann man es auch als Seriell-nach-Parallel-Konverter verwenden. D.h. eine serielle Eingabe (S_in) wird in eine parallele Ausgabe (Q_0:N-1) konvertiert.

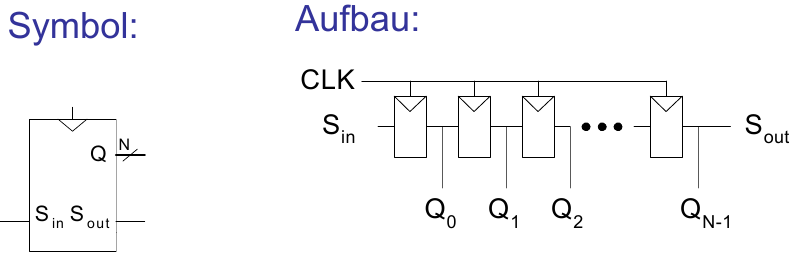
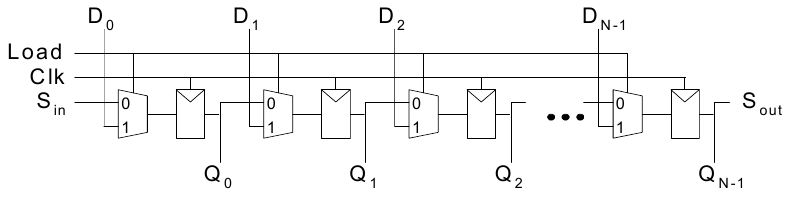
Schieberegister mit parallelem Laden

Ist das Signal Load = 1, agiert die Schaltung als normales N-bit Register. Ist Load = 0, agiert die Schaltung als Schieberegister. Dadurch ist sie verwendbar als Seriell-nach-Parallelkonverter (S_in nach Q_0:N-1) und Parallel-nach-Seriellkonverter (D_0:N-1 nach S_out).

Speicherfelder

Speicherfelder können effizient größere Datenmengen speichern. Dabei gibt es drei weitverbreitete Typen:

• Dynamischer Speicher mit wahlfreiem Zugriff (Dynamic random access memory, DRAM)
• Statischer Speicher mit wahlfreiem Zugriff (Static random access memory, SRAM)
• Nur-Lesespeicher (Read only memory, ROM)

An jede N-bit Adresse kann ein M-bit breites Datum geschrieben werden.

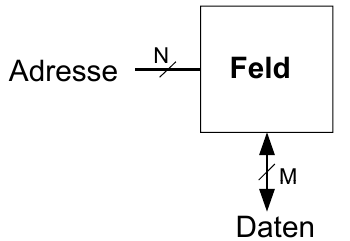
Speicherfelder sind zweidimensionale Felder von Bit-Zellen, wobei jede Bit-Zelle genau 1 Bit speichert.

Ein Feld hat N Adressbits und M Datenbits

• Zeilen und M Spalten
• Tiefe: Anzahl von Zeilen (Anzahl von Worten)
• Breite: Anzahl von Spalten (Bitbreite eines Wortes)
• Feldgröße Tiefe x Breite =

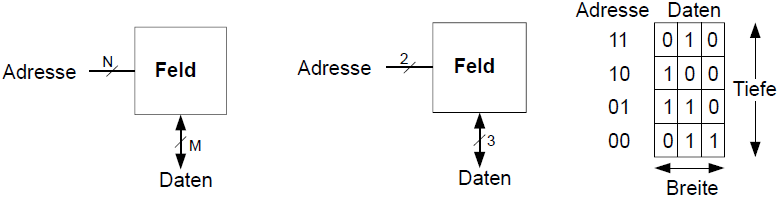
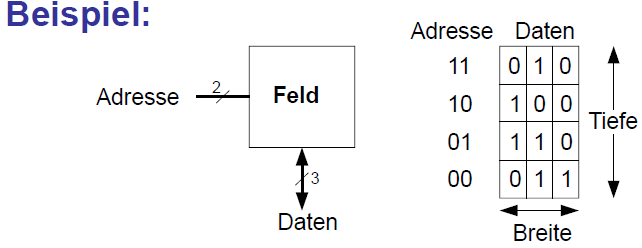
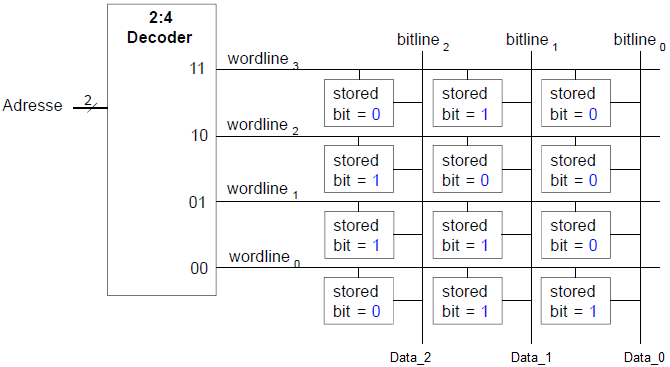
Beispiel Speicherfeld

• x 3-Bit Feld
• Anzahl Worte: 4
• Wortbreite: 3-Bit
• Beispiel: 3-Bit gespeichert an Adresse 2'b10 ist 3'b100

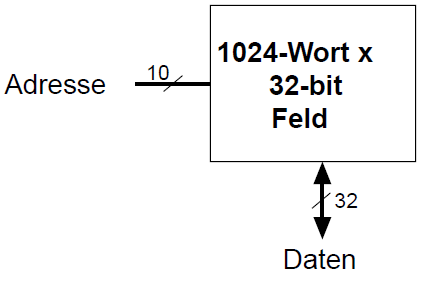
Aufbau von Speicherfeldern aus Bit-Zellen

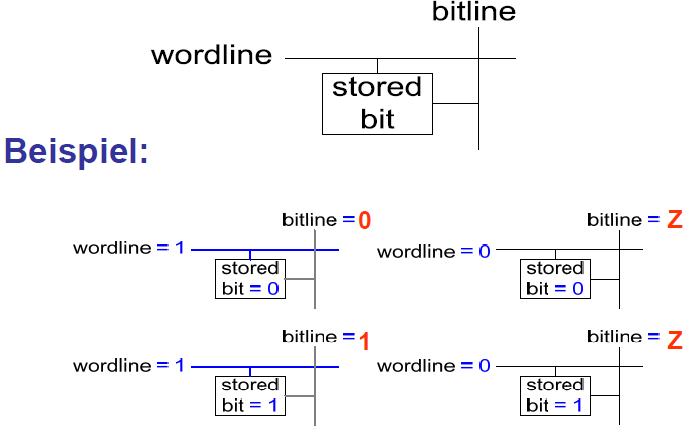
Wordline:

• Vergleichbar mit einem Enable-Signal
• Erlaubt Zugriff auf eine Zeile des Speichers zum Lesen oder Schreiben
• Entspricht genau einer eindeutigen Zeile
• Maximal eine Wordline ist zu jedem Zeitpunkt HIGH

Arten von Speicher: Historische Sicht

• Speicher mit wahlfreien Zugriff (RAM)
• Nur-Lese Speicher (ROM)

RAM: Random-Access Memory

• Flüchtig: Speicherinhalte gehen bei Verlust der Betriebsspannung verloren
• Kann i.d.R. schnell gelesen und geschrieben werden
• Zugriff auf beliebiger Adresse mit ähnlicher Verzögerung möglich
• Hauptspeicher moderner Computer ist dynamischer RAM (DRAM), genauer DDR3-SDRAM (Double Data Rate 3 - Synchronous Dynamic Random Access Memory)
• Name "RAM" ist historisch gewachsen, da früher (Bandspeicher, Trommelspeicher, Ultraschall-Laufzeitspeicher) unterschiedliche Zugriffszeiten für unterschiedliche Teile des Speichers galten

ROM: Read-Only Memory

• Nicht flüchtig: Erhält Speicherinhalte auch ohne Betriebsspannung
• schnell lesbar
• schreibbar nur sehr langsam (wenn überhaupt)
• Flashspeicher ist in diesem Sinne ein ROM (Cameras, Handys, MP3-Player)
• Erneut, Name historisch
• Kann ebenfalls von beliebigen Adressen gelesen werden
• Es gibt auch schreibbare Arten (PROM, EPROM, EEPROM, Flash)

Arten von RAM

Zwei wesentliche Typen:

• Dynamischer RAM (DRAM)
• Statischer RAM (SRAM)

Verwenden unterschiedliche Speichertechniken für die Bit-Zellen:

• DRAM: Kondensator
• SRAM: Kreuzgekoppelte Inverter

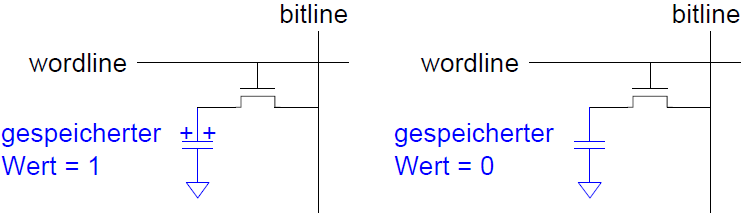
DRAM Bit-Zelle

Datenbit wird als Ladung eines Kondensators interpretiert. Dynamisch, da der Speicherwert periodisch neu geschrieben werden muss.

• Auffrischung alle paar Millisekunden nötig (üblicherweise 64ms)
• Kondensator verliert Ladung durch Leckströme
• ... und beim Auslesen!

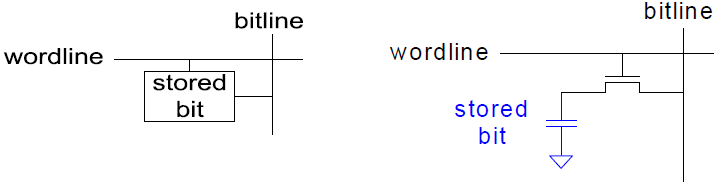
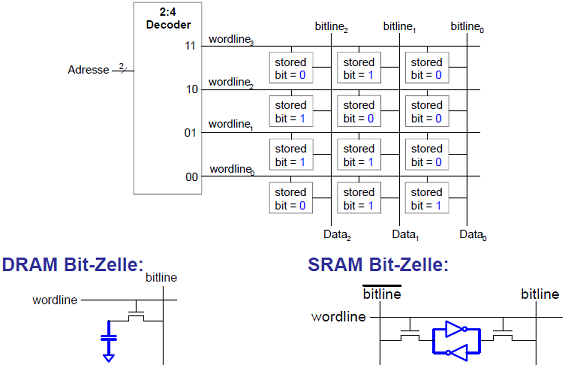
SRAM Bit-Zelle

• Datenbit wird als Zustand von rückgekoppelten Invertern gespeichert
• Statisch: keine Auffrischung nötig (Inverter treiben Pegel auf gültige Werte)

Bit-Zellen zusammengefasst:

ROM Bit-Zellen Aufbau:

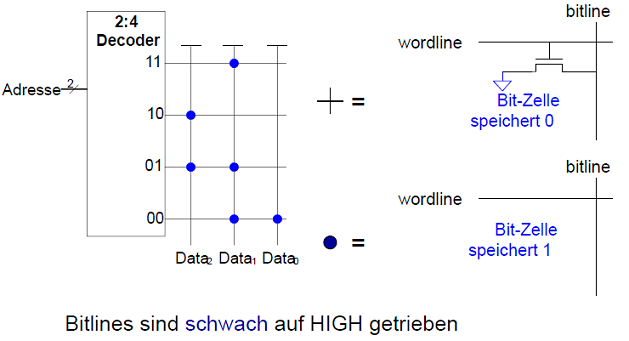
Flash-Speicher Bit-Zelle:

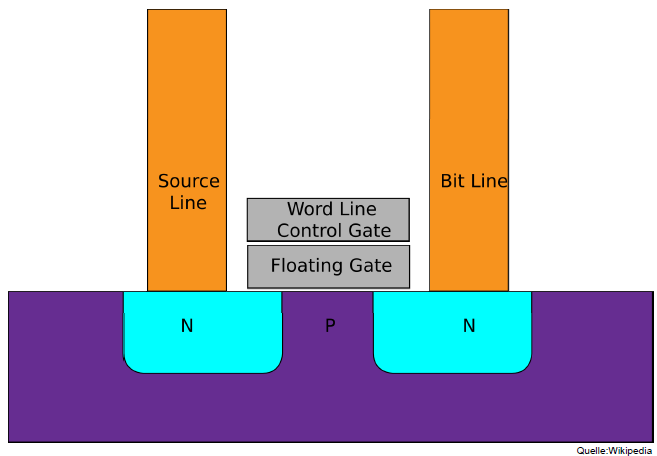
ROM als Datenspeicher:

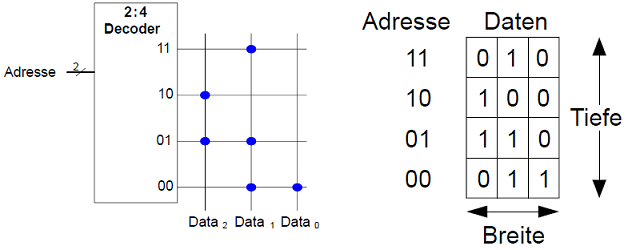
ROM als Wertetabelle für logische Schaltungen

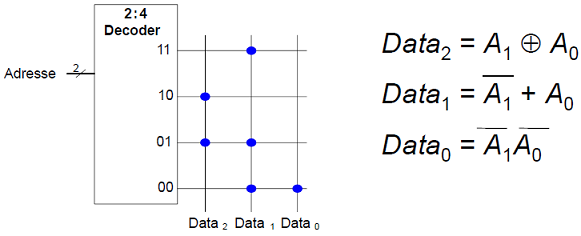
Beispiel: Logik aus ROMs

Implementierung der folgenden logischen Funktionen auf einem Bit ROM:

• 
• 
• 

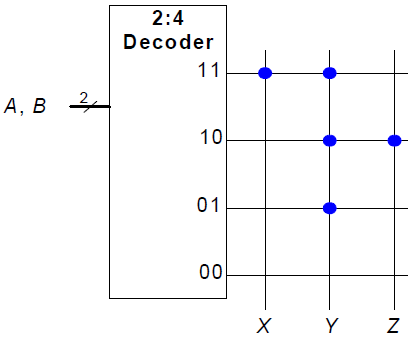
Beispiel: Logik aus beliebigem Speicherfeld:

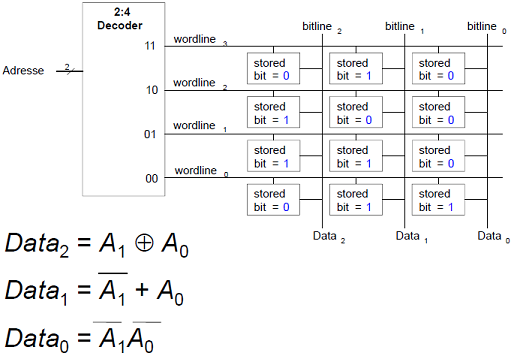
Implementierung der folgenden logischen Funktionen durch Bit ROM:

• 
• 
• 

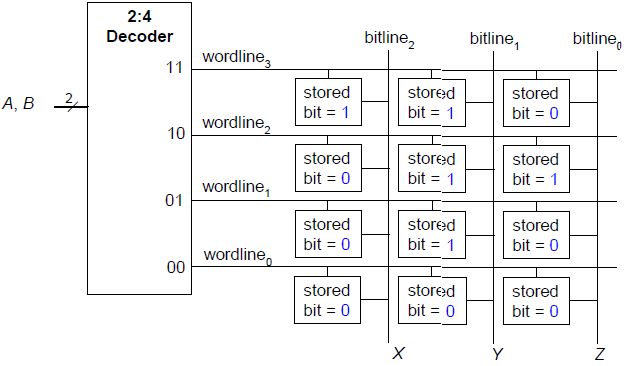
Ändere Funktion nur durch Ändern der Speicherinhalte!

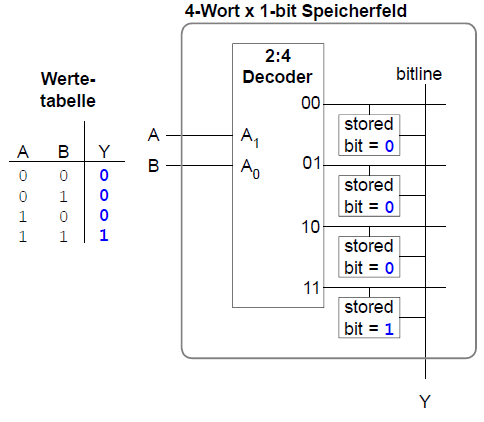
Speicherfelder speichern Wertetabellen

• Look-Up Tables (LUT)

Wort aus Eingangsvariablen bildet Adresse

Für jede Kombination von Eingangswerten ist der Funktionswert gespeichert.

Multi-Port-Speicher

Ein Port besteht aus zusammengehörigen Anschlüssen für Adresse und Datum. Dabei besteht ein Drei-Port Speicher aus

Kleine Multi-Port-Speicher werden als Registerfelder bezeichnet. Diese werden z.B. in Prozesooren eingesetzt.

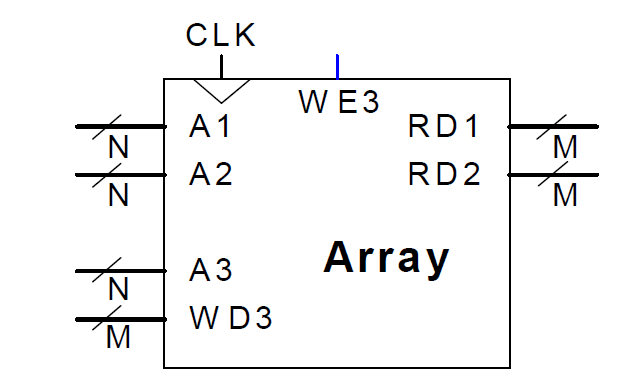
Speicherfeld in Verilog

Logikfelder (logic arrays)

• Programmable Logic Arrays (PLAs)

• Field Programmable Gate Arrays (FPGAs)

Boole'sche Funktionen mit PLAs: Idee

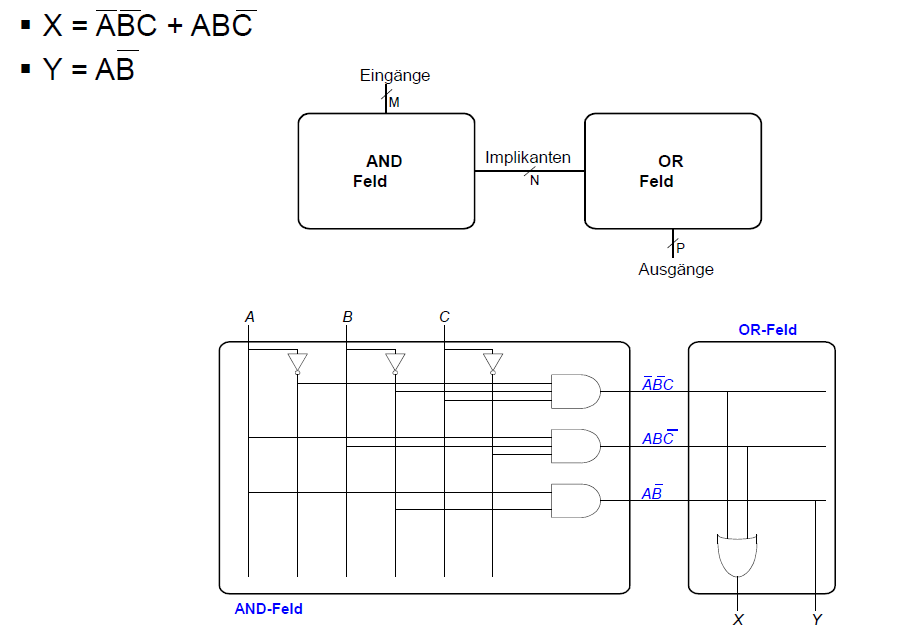
PLAs: Vereinfachte Schreibweise

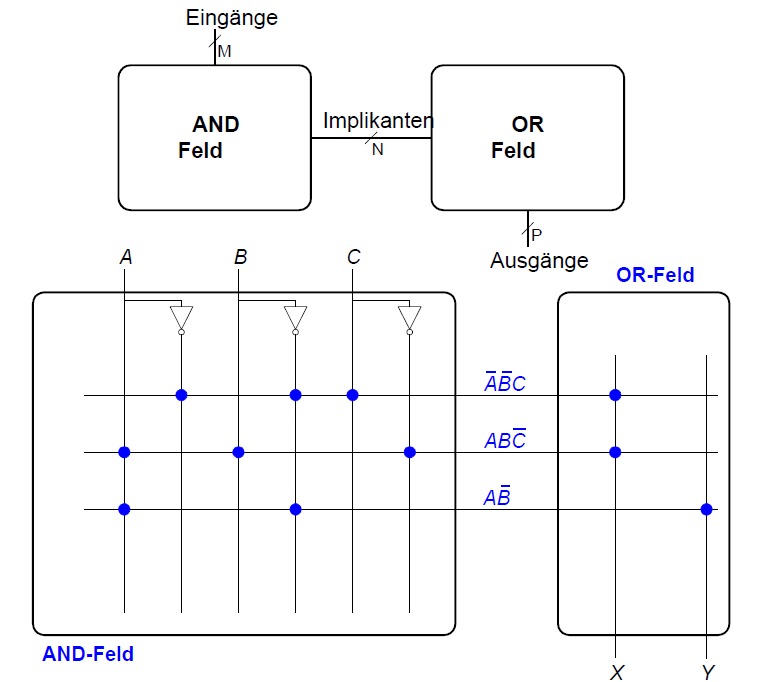
FPGAs: Field Programmable Gate Arrays

FPGAs bestehen grundsätzlich aus:

• CLBs (Configurable Logic Blocks): Realisieren kombinatorische und sequentielle Logik. Es sind also konfigurierbare Logikblöcke
• IOBs (Input/Output Blocks): Schnittstelle vom Chip zur Außenwelt. Also Ein-/Ausgabeblöcke.
• Programmierbares Verbindungsnetz: Verbindet CLBs und IOBs. Dies kann flexible Verbindungen je nach Bedarf der aktuellen Schaltung herstellen.
• Reale FPGAs enthalten oftmals noch weitere Arten von Blöcken
• RAM
• Multiplizierer
• Maninpulation von Taktsignalen (DCM)
• Sehr schnelle serielle Verbindungen (11 Gb/s)
• Komplette Mikroprozessoren
• ...

Struktur eines Xilinx Spartan 3 FPGA

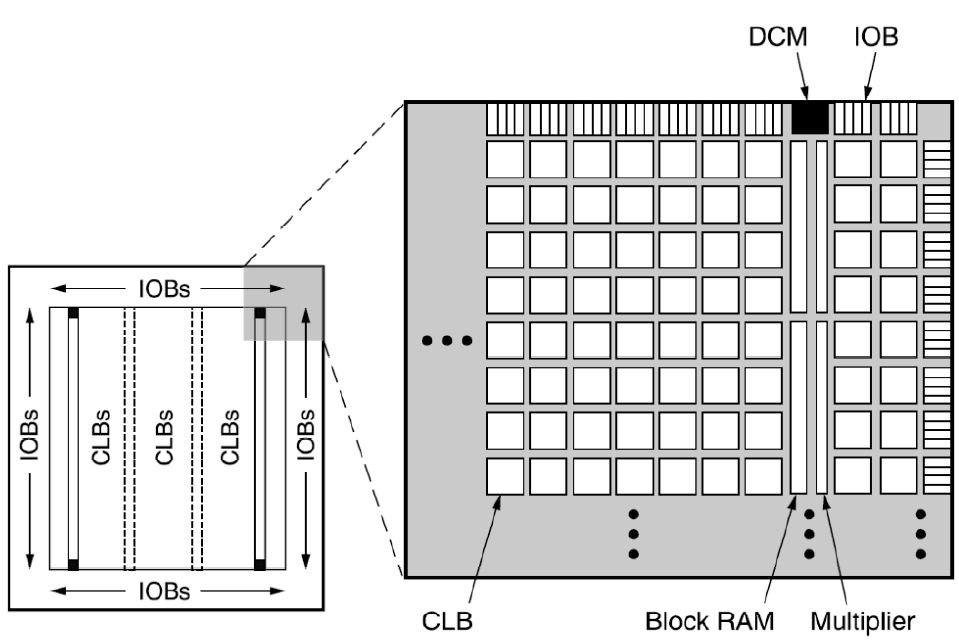
Konfigurierbare Logikblöcke (CLBs)

CLBs bestehen im wesentlichen aus:

• LUTs (lookup tables): realisieren kombinatorische Funktionen
• Flip-Flops: realisieren sequentielle Funktionen
• Multiplexern: Verbinden LUTs und Flip-Flops

Xilinx Spartan 3 CLB

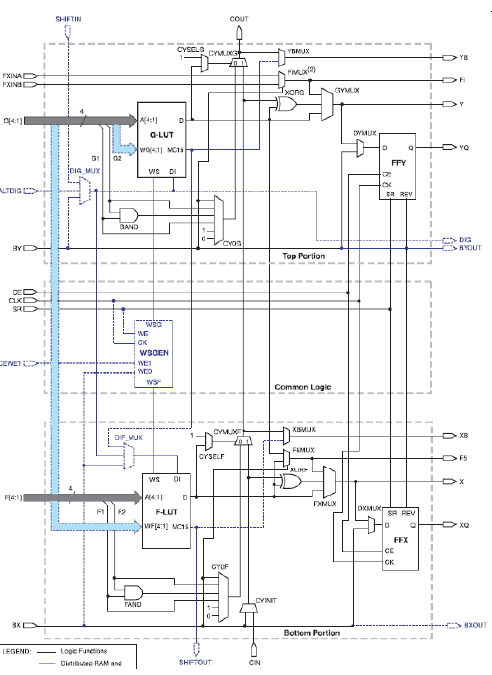
Xilinx Spartan CLB

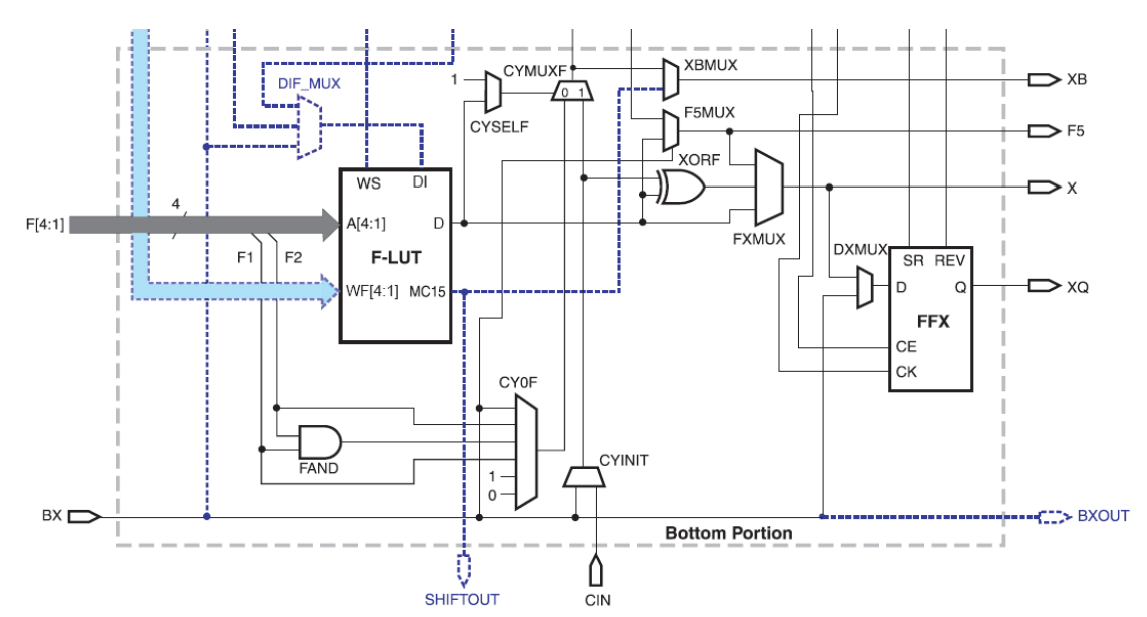
Ein Spartan 3 CLB enthält:

* 2 LUTs:

* 2 sequentielle Ausgänge:

* 2 kombinatorische Ausgänge:

Beispiel: Kombinatorische Logik mit CLBs

Berechnung der folgenden Funktionen mit dem Spartan 3 CLB

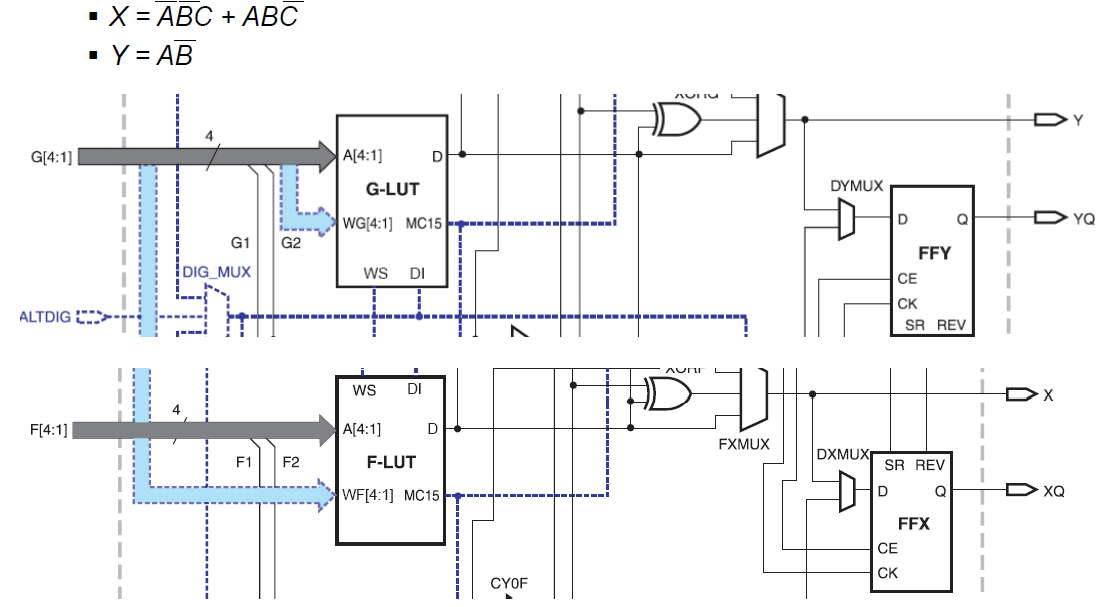
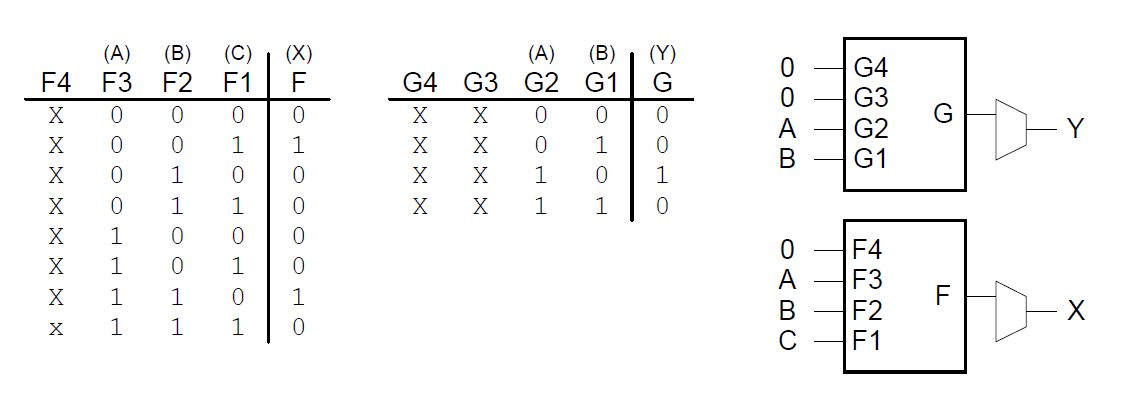
Entwurfsfluss für FPGAs

Der Enwurfsfluss wird in der Regel durch Entwurfswerkzeuge wie Xilinx ISE unterstützt. Dies ist in der Regel ein iterativer Prozess, bestehend aus:

• Planen
• Implementieren
• Simulieren
• Wiederholen...

Der Entwickler denkt nach, gibt einen Entwurf als Schaltplan oder HDL-Beschreibung ein und wertet die Simulationsergebnisse aus. Wenn die Simulation zufriedenstellend ist, dann wird der Entwurf als Netzliste synthetisiert (eine textuelle Beschreibung der elektrischen Verbindungen zwischen Bauelementen). Die Netzliste wird auf die FPGA-Konfiguration abgebildet (CLBs, IOBs, Verbindungsnetz). Danach werden die Konfigurationsdaten (bit streams) auf den FPGA geladen und zum Schluss in realer Hardware getestet.